Dacă ar trebui să prezint după metoda științei spiritului ceea ce am de spus, ar trebui să pornesc desigur de la alte premise și într-un fel am putea ajunge chiar mai repede la ținta spre care vrem să ne îndreptăm. O astfel de tratare nu v-ar fi putut satisface însă tocmai în ceea ce constituie intenția acestor conferințe, fiindcă aici se pune problema de a realiza o punte cu modul de gândire științific obișnuit, deși pentru aceste expuneri am selectat în mod expres capitole unde această punte se realizează greu datorită modului de gândire obișnuit, departe de un punct de vedere conform cu realitatea. Și chiar dacă trebuie combătut punctul de vedere nerealist, prin această combatere vom putea vedea tocmai cum putem scăpa de insuficiențele teoriilor moderne și cum ne putem însuși o modalitate de înțelegere realistă a lucrurilor despre care vorbim. De aceea eu aș dori să mă refer astăzi la felul cum s-au format în ultima vreme reprezentările despre fenomenele cerești.
În ceea ce privește formarea acestor reprezentări trebuie să deosebim două lucruri: mai întâi că aceste reprezentări au la origine observații, observații asupra fenomenelor cerești, și că asupra acestor observații s-au făcut considerații teoretice abia ulterior. Uneori, pe baza câtorva observații, relativ puține, s-au brodat teorii foarte stufoase. Acesta este un fapt – că s-a pornit de la observații și prin intermediul lor s-a ajuns la anumite reprezentări. Celălalt aspect este însă că, după ce s-a ajuns la anumite reprezentări, acestea s-au transformat în ipoteze. Dar în emiterea ipotezelor, care după aceea ajung să stabilească o anumită imagine foarte precisă, de cele mai multe ori domnește arbitrarul absolut, deoarece în formarea teoriilor se impune cu predilecție prejudecata existentă la una sau alta dintre personalitățile care construiesc asemeneă teorii.
Aici vreau să vă atrag atenția în primul rând asupra unui lucru care probabil pentru început vi s-ar părea paradoxal, dar care pe parcursul cercetării următoare trebuie să se dovedească extrem de fecund, dacă este privit cu exactitate. Vedeți dumneavoastră, în întreaga gândire naturalist-științifică modernă domnește ceea ce s-ar putea numi, și de altfel s-a și numit, regula philosophandi [Nota 38]. Ea constă în aceea că se spune: Ceea ce s-a explicat pe baza unei anumite cauzalități într-un domeniu al realității, trebuie explicat la fel și în alte domenii ale existenței, ale realității pornindu-se de la aceleași cauze. De obicei când se stabilește o astfel de regula philosophandi se pornește de la ceva foarte clar, de la ceva de la sine înțeles. Așa, de exemplu, putem spune, precum newtonienii de altfel: Procesul de respirație trebuie să aibă aceleași cauze la animal ca și la om, aprinderea unei surcele trebuie să aibă aceeași cauză, fie că se produce în Europa, fie că se produce în America. – Până aici lucrurile rămân absolut în sfera evidenței. După aceea însă se face un salt, care nu se remarcă și se acceptă ca fiind de la sine înțeles. Acest lucru ne apare dacă privim un aspect legat chiar de aceste personalități, afectate de acest mod de gândire. Se spune: Dacă luăm o lumânare care arde și Soarele care luminează, atunci la baza luminii dată de lumânare și a luminii dată de Soare trebuie să stea aceeași cauză. Dacă o piatră cade pe Pământ și dacă Luna se învârte în jurul Pământului, atunci la baza mișcării pietrei și a mișcării Lunii trebuie să se găsească aceeași cauză. – În legătură cu o astfel de gândire mai trebuie adaugat și altceva: nu s-ar ajunge la nici o explicație în domeniul astronomiei dacă lucrurile nu s-ar petrece astfel, fiindcă nu putem obține explicații doar [Nota 39] despre ceva ce ține de pământesc. Dacă deci în depărtările spațiului ceresc nu ar domni aceeași cauzalitate ca pe Pământ, nu s-ar putea ajunge la nici o teorie.
Vă rog însă să observați că această regula philosophandi, care a fost expusă aici, nu este în ultimă instanță decât o prejudecată. Căci cine în lumea asta garantează că, într-adevăr, la baza luminii dată de lumânare și a celei dată de Soare se află aceleași cauze; sau că la baza căderii unei pietre sau a căderii vestitului măr din copac, prin care Newton a ajuns la teoria sa, se află aceleași cauze ca în situația mișcării corpurilor cosmice? Este desigur un lucru care trebuia amintit de la început. Aceasta nu este decât o prejudecată. Și astfel de prejudecăți se strecoară în special acolo unde se încearcă să se brodeze, întâi prin inducții, niște considerații teoretice, niște reprezentări imaginative legate de anumite observații, după care se trece orbește la deducții, prin care se construiesc tot felul de sisteme cosmice.
Ceea ce vă înfățișez aici atât de abstract a devenit însă un fapt istoric. Fiindcă, vedeți dumneavoastră, în ceea ce au scos marile spirite la începutul vremurilor moderne – Copernic, Kepler, Galilei – din câteva observații pe care le-au făcut, putem urmări o evoluție continuă. Și trebuie să spunem că la Kepler, în legea a treia amintită ieri, se găsește ceva cu totul ieșit din comun în ceea ce privește analiza faptelor care îi puteau sta doar lui la dispozitie. Este activată aici, în cazul lui Kepler, o enormă tensiune spirituală, atunci când din puținele date aflate la dispoziția sa a găsit această, să-i zicem, „lege” – mai bine zis concluzie noțională – privitoare la fenomenele cosmice. După aceea însă începe o evoluție care trece prin Newton și care nu pornește propriu-zis de la observații reale, ci chiar de la aspectele teoretice și construiește tot felul de noțiuni de forță și masă, pe care de fapt, dacă vrem să rămânem în realitate, ar trebui să le lăsăm deoparte. Și tot acest proces se continuă până la un punct culminant, când apare într-un mod deosebit de ingenios, chiar genial, într-o concepție care vrea să explice geneza sistemului cosmic, cum ar fi cazul lui Laplace [Nota 40] în celebra lui carte Exposition du systeme du monde sau a lui Kant în cartea sa Naturgeschichte und Theorie des Himmels*. Și în tot ceea ce a urmat mai departe pe parcursul evoluției vedem făcându-se încercarea de a se explica deductiv, pe baza reprezentărilor făcute asupra interdependenței mișcărilor cerești, nașterea sistemului cosmic prin acea ipoteză a nebuloasei originare și așa mai departe.
* Istorie naturală și teoria cerului. [Nota 41]
Acest lucru trebuie observat în special în istoria evoluției: faptul că în cursul ei apare ceva alcătuit din inducții, formulate genial fără doar și poate, chiar în acest domeniu, și din deducții ulterioare, în care însă este antrenat foarte mult ceva din ceea ce au considerat important respectivele personalități, după propria lor înclinație. Astfel că putem spune: Atâta timp cât unul din ei gândea materialist, pentru el era absolut legitim să amestece în noțiunea deductivă reprezentări materialiste. Căci acolo nu mai operau faptele. Acolo se putea porni doar de la teoria care rezulta în urma unei deducții. Și în felul acesta putem spune, de exemplu: Se construia exclusiv inductiv reprezentarea, ce se putea rezuma într-o noțiune de genul: în centru – Soarele, planetele gravitând în jurul lui după traiectorii eliptice, conform unei anumite legi, lege care spune că razele vectoare parcurg sectoare egale în timpi egali. Și în timp ce privirea se îndrepta asupra fiecărei planete din sistemul solar, se putea formula, pe de altă parte, prin legea a treia a lui Kepler, relația lor reciprocă: Raportul pătratelor perioadelor de revoluție ale diferitelor planete este egal cu raportul cuburilor distanțelor medii ale acestora față de Soare. Aceasta crea o anumită imagine. Problema nu era însă decisă, dacă această imagine conținea în sine o suprapunere completă cu realitatea, sau era o abstracțiune extrasă din realitate. Prin aceasta nu era redat felul cum se raportează această imagine la totalitatea realului, dar din această imagine, și nicidecum din realitate, ci din această imagine se deducea tot ceea ce ulterior a devenit în fond o astronomie genetică. Acest fapt trebuie avut în vedere în primul rând. Iar omul din ziua de azi este educat din copilărie, ca și cum tot ceea ce s-a dedus vreme de câteva secole încoace ar corespunde unei realități.
De aceea să facem abstracție de tot ceea ce este pur ipotetic și teoretic în acest proces evolutiv, rămânând, în măsura în care se poate, în sfera a ceea ce este cu adevărat științific, și să luăm reprezentările care nu se îndepărtează de realitate atât de mult încât să nu mai putem descoperi mai târziu legătura lor cu realitatea. Sarcina mea în toată expunerea de astăzi va fi deci să mă mișc în direcția în care s-a mișcat gândirea modernă în aceste domenii, dar numai într-atât cât să pot ajunge, tocmai pentru a mă menține în sfera științificului, până la forma noțiunilor, care, ulterior, dacă le luăm ca noțiuni, să ne mai permită să regăsim drumul înapoi la realitate. Nu vreau deci să mă îndepărtez de realitate și noțiunile să devină așa de rudimentare, încât să putem deduce din ele ipoteze de nebuloase originare.
Dacă vom proceda astfel în expunerea noastră de astăzi, vom putea spune: Dacă urmărim acest fel modern de elaborare a noțiunii pe tărâmul de care ne ocupăm, atunci va trebui întâi să construim noțiunea într-adevăr inductiv, așa cum i-a rezultat ea lui Kepler și cum a fost dezvoltată ulterior și apoi s-o privim cu atenție. Fac în mod expres încă o dată observația că în ceea ce privește aceste noțiuni nu vreau să merg decât până acolo unde noțiunea, oricât de complicată ar fi, chiar falsă, este încă destul de aproape de realitate, ca să se poată elimina din ea ceea ce este fals și să se poată ajunge din nou la ceea ce este just. Se pune problema să dezvoltăm un anumit tact în a reusi să sesizăm bruma de realitate din noțiunile care se elaborează. Nu se poate proceda altfel, dacă vrem să realizăm o punte între ceea ce corespunde realității și spiritul științific, învăluit în teoriile moderne.
În primul rând avem o noțiune asupra căreia trebuie să zăbovim puțin: planetele au traiectorii excentrice, descriu elipse. Este primul lucru pe care îl putem susține: planetele au traiectorii excentrice și descriu elipse; în unul dintre focare se găsește Soarele, iar ele descriu aceste elipse conform legii că razele vectoare parcurg sectoare egale în intervale de timp egale.
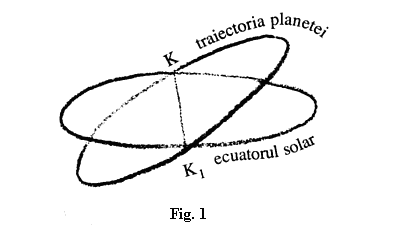
Al doilea aspect important este că în reprezentare constatăm că pentru fiecare planetă există un singur plan al traiectoriei. Chiar dacă în general planetele se rotesc în apropiere una de alta, totuși pentru fiecare planetă există un plan al traiectoriei propriu, înclinat față de planul ecuatorial solar [Nota 42]. Simplu deci: dacă în figura 1 desenăm planul ecuatorului solar, planul orbitei unei planete ar fi înclinat și nu ar coincide sub nici o formă cu planul ecuatorului solar.
Acestea sunt două reprezentări foarte importante care se pot construi din observațiile făcute. Și de îndată ce îți formezi aceste reprezentări trebuie luat în considerare ceva care, în imaginea reală a lumii, se împotrivește – așa zicând – acestor reprezentări. Astfel, dacă încercăm să ne imaginăm simplu sistemul nostru solar în totalitatea sa, și pentru aceasta luăm ca bază doar aceste două reprezentări: planetele se deplasează pe orbite excentrice, iar planurile acestor orbite sunt înclinate diferit față de planul ecuatorului solar, atunci, de îndată ce ai vrea să extrapolezi aceasta ca o lege, nu te mai descurci sub nici o formă când este vorba de mișcările cometelor. Când iei în discuție aceste mișcări, nu mai ajungi la nici un rezultat, reprezentările sunt insuficiente. Iar urmările le puteți înțelege mai degrabă cu ajutorul faptelor istorice, decât prin considerații teoretice.
Din reprezentările amintite, potrivit cărora planurile traiectoriilor planetelor se află aproximativ în planul ecuatorului solar și traiectoriile planetelor sunt elipse excentrice, din chiar aceste reprezentări Kant, Laplace și urmașii lor au formulat ipoteza nebuloasei originare. Și acum să urmărim ce a ieșit de aici. La nevoie – și numai la nevoie – se poate înfățișa un fel de istorie a genezei sistemului solar. Dar tot acest sistem cosmic care s-a elaborat nu conține de fapt nicăieri o explicație cât de cât satisfăcătoare asupra participării pe care o au aici cometele. Ele întotdeauna fac excepție de la teorie. Această excepție de la teorie, așa cum constatăm pe cale istorică, este o dovadă a împotrivirii vieții cometare la acea noțiune care nu este construită din totalitatea fenomenelor, ci doar dintr-o parte a acestei totalități. Apoi trebuie să ne fie clar faptul că aceste comete în traiectoriile lor coincid frecvent cu alte corpuri, care intervin, de asemenea, în sistemul nostru solar și care prin însăși calitatea lor de însoțitori ai cometelor constituie o enigmă. Acestea sunt roiurile de meteoriți, care coincid deseori ca traiectorie cu traiectoria cometei. Vedem deci aici intervenind ceva în ansamblul sistemului nostru, care ne face să spunem: Din observarea totalității sistemului nostru s-a format treptat o sumă de reprezentări, care nu ne ajută să stăpânim un aspect oferit de cometele și de roiurile de meteoriți ce străbat sistemul nostru în mod foarte neregulat, aproape arbitrar. Acestea se sustrag în special acelei înțelegeri formulate pe baza reprezentărilor abstracte care s-au acumulat. Ar trebui să vă fac o disertație istorică lungă, dacă ar fi să vă prezint în amănunt greutățile care apar concret atunci când cercetătorii, sau mai bine spus gânditorii, ajung la comete și roiuri de meteoriți pornind de la teorii astronomice. De fiecare dată nu voi indica decât niște direcții în care putem căuta gândirea sănătoasă. La această gândire sănătoasă ajungem dacă mai luăm în considerare si altceva.
Acum trebuie să încercăm ca din noțiunile reale care au mai rămas, adică acelea care mai au în ele un rest de realitate, să ne întoarcem din nou puțin înapoi. Acest lucru trebuie făcut de fiecare dată vizavi de lumea exterioară, pentru ca noțiunile să nu se îndepărteze prea mult de realitate. Omul are tendința să facă acest lucru. Trebuie să ne întoarcem mereu înapoi. Când ți-ai formulat noțiunea: Planetele se deplasează pe traiectorii eliptice, și când pe baza acestei noțiuni începi să construiești o teorie, deja este extraordinar de periculos. Este mult mai bine ca, după ce ți-ai format o astfel de noțiune, să revii din nou la realitate și să verifici dacă nu trebuie să corectezi, sau măcar să modifici acea noțiune. Este lucrul cel mai important. Aceasta apare foarte clar. În gândirea biologică și în cea medicală această eroare se practică atât de des, încât nu se mai face niciodată ceea ce este necesar, adică nu se mai ține cont ca, după ce ți-ai format o noțiune, să revii imediat la realitate și să vezi dacă nu trebuie să faci unele modificări.
Deci planetele se mișcă pe elipse, dar aceste elipse sunt variabile, câteodată ele sunt mai mult cercuri, altă dată mai mult elipse. Acest lucru îl întâlnim iar, dacă revenim cu noțiunea de elipsă la realitate. În timp, o elipsă devine ceva mai bombată, tinde mai mult spre cerc, după care ea tinde din nou să devină elipsă. Deci când spunem că planetele se mișcă pe elipse faptul nu cuprinde deloc întreaga realitate; și atunci eu trebuie să modific noțiunea. Va trebui să spun: Planetele se deplasează pe traiectorii care duc continuu o luptă între tendința de a deveni cerc și tendința de a rămâne elipsă. Dacă acum trasez această curbă (elipsa), va trebui, pentru a aprecia just noțiunea, să fac curba din cauciuc, sau cel puțin să o fac mobilă, ar trebui să o modific permanent. Căci stabilind elipsa pentru o rotație a planetei, ea nu se mai potrivește și pentru următoarea rotație, și cu atât mai puțin cu următoarele. Cu alte cuvinte lucrurile nu sunt chiar așa de simple încât, trecând de la realitate la rigiditatea unei noțiuni, să mai rămân încă în realitate. Acesta este un aspect.
Celălalt aspect este următorul: planurile traiectoriilor planetelor, așa cum am mai spus, sunt înclinate față de planul ecuatorului solar. Deoarece planetele în punctele de intersecție a planelor trec în sus sau în jos, spunem că formează noduri. Nici acestea nu sunt puncte fixe. Dreptele care unesc aceste noduri (KK1 din fig. 1) sunt mobile, ca de altfel și înclinațiile planurilor unul față de celălalt. Deci chiar și aceste înclinații, când le exprimăm în formule noționale, ne aduc din nou la o noțiune rigidă, pe care trebuie să o modificăm imediat conform realității. Dacă o dată traiectoria este înclinată într-un fel, iar altă dată în alt fel, prin aceasta se modifică tot ceea ce s-a conceput prima dată ca noțiune. Sigur, odată ajunși în acest punct putem deveni comozi și să spunem: Fără doar și poate, în realitate există perturbații, noi nu reușim să cuprindem realitatea cu noțiunile noastre, decât aproximativ. – După care continuăm să înotăm comod în teorii. Dar în felul acesta înotăm până când, tot încercând să construim din aceste teorii imagini fanteziste care să corespundă realității, ele nu mai corespund acestei realități.
Este desigur ușor de admis că această variație a traiectoriilor excentrice, a înclinărilor planelor planetelor trebuie să aibă oarecum o legătură cu viața sistemului planetar în ansamblu, sau, cum am spune noi, cu activitatea din întregul sistem planetar. Este un lucru de la sine înțeles că acestea trebuie să depindă într-un fel de întreaga activitate a sistemului nostru planetar. Însă dacă acum, pornind de aici, se construiește din nou noțiunea, adică spunem: Foarte bine, îmi voi pune deci și eu gândirea în mișcare, astfel încât să-mi imaginez elipsa bombându-se și îngustându-se continuu, planul orbitei suind și coborând, rotindu-se, atunci voi putea să construiesc din nou un sistem planetar apropiat de realitate. – Foarte frumos. Însă dacă mergeți cu noțiunea până la capăt obțineți, chiar dacă gândiți foarte consecvent, un sistem planetar care nu poate dura în timp. Prin însumarea perturbațiilor care apar și în special datorită variabilității nodurilor, sistemul planetar se apropie tot mai mult de moartea sa, de un imobilism. Dar acum intervine ceea ce au accentuat întotdeauna filosofii [Nota 43]: dacă ne imaginăm un astfel de sistem, realitatea ar fi avut destul timp să ajungă la punctul final. Nu există nici un motiv pentru ca acest lucru să nu se fi întâmplat până acum. Am fi avut de-a face cu un infinit încheiat, ajuns la capăt, și imobilismul ar fi trebuit să fie deja prezent. Intrăm într-un domeniu în care, trebuie să ne fie clar, gândirea parcă se oprește în loc. Căci tocmai prin faptul că merg cu gândirea până la punctul final obțin un sistem cosmic în repaus, imobil. Dar ceea ce am obținut astfel nu este ceva real.
Acum se mai întâmplă ceva, și de acest lucru trebuie neapărat ținut seamă. Dacă urmărim lucrurile în continuare, în special la Laplace [Nota 44] – eu vreau de fiecare dată să prezint doar fenomenele –, vedem că acest sistem cosmic nu ajunge în starea de repaus sub influențele perturbatoare ale variabilității nodurilor, deoarece rapoartele perioadelor de revoluție ale planetelor sunt mărimi incomensurabile, sunt numere cu infinit de multe zecimale. Deci ajungem să spunem: Dacă, în sensul legii a treia a lui Kepler, comparăm perioadele de revoluție ale planetelor, rapoartele acestor perioade nu se pot indica prin numere întregi și nici prin fracții finite, ci doar prin numere incomensurabile, numere care nu au niciodată sfârșit. De aceea și astronomia actuală a ajuns la concluzia că sistemul planetar își datorează starea de mișcare și acestui fapt, al incomensurabilității rapoartelor perioadelor de revoluție, din legea a treia a lui Kepler, căci altfel de mult ar fi trebuit să ajungă în repaus.
Dar să reținem acum foarte exact un lucru. Am ajuns în final ca noțiunile pe care ni le-am format despre sistemul planetar să le fixăm în niște numere, care nu pot fi înțelese în nici un chip. Este un fapt extrem de important. Am ajuns deci, printr-o necesitate a procesului științific însuși, să gândim matematic sistemul planetar, dar în așa fel încât acest matematic nu mai este ceva care să se poată măsura. Iar acolo unde, în evoluția matematică, apare o incomensurabilitate ne aflăm în punctul, în momentul, unde trebuie totuși să acostăm la un număr comensurabil. Oprim pe loc numărul incomensurabil, scriem fracția zecimală [Nota 45] respectivă, dar numai până la un anumit punct. La un moment dat, când ajungem la incomensurabil, părăsim ceea ce am făcut până atunci. Aceia dintre dumneavoastră care sunt matematicieni pot înțelege despre ce este vorba, și anume că în cazul numărului incomensurabil este ceva care mă face să spun că matematizez până aici, după care afirm: De aici nu mai merge. – Nu pot compara aceasta, faptul că în matematică trebuie la un moment dat să mă opresc, decât cu – ierați-mă dacă folosesc o comparație puțin comică pentru ceva serios – o scenă la care am asistat o dată la Berlin. Era atunci la modă varieteul, apărut prin contribuția câtorva oameni, unul din ei fiind Peter Hille [Nota 46]. El întemeiase o estradă și voia să-și recite acolo propriile poezii. Era un om foarte drăguț, în fondul lui intim era un teosof adevărat, dar ceva la stilul boem. O dată am fost și eu la o reprezentație de estradă, unde el își recita propria operă poetică. Aceste poezii aveau toate rândurile compuse până la capăt, dar el citea cam în felul următor:
„Soarele apunea.., și așa mai departe” – primul rând
„Luna răsărea... și așa mai departe” – era al doilea rând.
La fiecare rând el spunea: și așa mai departe, și tot așa! În aceasta a constat recitarea la care am asistat atunci. În fond era ceva cât se poate de incitant. Fiecare putea completa rândurile după cum voia. Nu la fel stau lucrurile în cazul numerelor incomensurabile, totuși, când suntem pe tărâmul incomensurabilității, ceva se aseamănă cu ceea ce am descris, prin faptul că procesul care urmează nu poate fi decât sugerat. Nu putem spune decât: Trebuie mers în direcția aceasta. Nu se dă nimic ca să-mi pot face o imagine despre ce fel de numere mai pot apărea aici. Este foarte important acest fapt, că atunci când este vorba despre domeniul astronomiei suntem conduși pe făgașul acestei incomensurabilități, că deci nu putem ajunge altundeva când ne ocupăm cu astronomia decât la granița matematicului, că pur și simplu realitatea ne scapă. Realitatea fuge de noi, ne scapă, altfel nu putem spune.
Dar ce înseamnă aceasta? Noi aplicăm matematica, cea mai sigură știință a noastră, la fenomenele cerești, dar aceste fenomene cerești nu se înclină în fața acestei științe foarte sigure, ele se strecoară la un moment dat printre degetele noastre. Și se furișează în domeniul incomensurabilității tocmai în ceea ce ține de viața lor. Astfel că aici, într-un anumit punct, se întâmplă să înceteze posibilitatea de a înțelege realitatea, această realitate intrând în haos. De aici încolo nu mai putem întreba: Ce face de fapt această realitate – pe care noi o urmărim aici matematizând – acolo unde se furișează în incomensurabil? – Cu siguranță acolo ea face ceva ce ține de facultatea de viață a ei. Dacă deci vrem să intrăm în realitatea astronomică, trebuie să ieșim din ceea ce stăpânim cu ajutorul matematicii. Acest fapt ni-l arată calculul însuși [Nota 47], ni-l arată însăși evoluția științei. Asupra acestor puncte trebuie insistat, dacă vrem să dezvoltăm spiritul în conformitate cu realitatea.
Și acum aș dori să vă înfățișez celălalt pol al problemei. Vedeți dumneavoastră, dacă o luați din punct de vedere fiziologic, puteți porni de la un anumit moment al evoluției embrionare, de exemplu al embrionului uman sau al oricărei alte ființe în luna a treia sau a doua de dezvoltare. Puteți să urmăriți această evoluție anterioară, după care, atât cât o permit mijloacele științifice de astăzi, puteți vedea – lucrul este posibil, de fapt, într-o măsură foarte-foarte mică, după cum vor fi știind aceia care s-au ocupat de această problemă –, puteți vedea, dacă există cât de cât reprezentări valabile, următorul fapt: se poate merge înapoi doar până la un anumit punct – și mult prea departe nu se poate ajunge –, acela al desprinderii ovulului, al ovulului nefecundat [Nota 48]. Încercați să vă reprezentați cât de departe puteți merge înapoi cu această urmărire. Dacă vreți să mergeți și mai în urmă, va trebui să vă întoarceți în nedefinitul organismului matern în ansamblu. Cu alte cuvinte, mergând așa înapoi veți intra într-un fel de haos. Acest fapt nu îl puteți evita cu nici un chip; că așa stau lucrurile îl arată din nou mersul dezvoltării științei. Vă rog să urmăriți doar ipotezele științifice care au apărut în panspermie [Nota 49] sau lucruri de genul acesta, unde s-au făcut tot felul de speculații, precum că fiecare ovul se prefigurează din forțele întregului organism, ceea ce corespundea concepției lui Darwin [Nota 50]0, sau că acest ovul se dezvoltă mai mult separat, în înseși organele sexuale și așa mai departe. În cadrul evoluției gândirii științifice din acest domeniu veți vedea că, urmărindu-se în sens invers această geneză a apariției ovulului în organismul matern, a ieșit la iveală o mulțime întreagă de ipoteze fanteziste privitoare la fenomenele care stau la baza acesteia. Aici intrari în echivocul absolut. Astăzi în știința exterioară privitoare la această chestiune nu există decât speculații despre legătura dintre ovul și organismul matern.
După aceea însă, la un moment dat, acest ovul apare bine conturat în ceva, care poate fi prins satisfăcător sub formă matematică, chiar dacă doar geometrizând. De la un punct încolo puteți chiar desena. În embriologie există astfel de desene. Ovulul, celula, le puteți desena, puteți, mai mult sau mai puțin, să le urmăriți dezvoltarea în mod real. În felul acesta putem începe să înfățișăm ceva, un fel de geometrie, ceva ce se poate cuprinde în forme. Aici se urmărește o realitate. Într-un anumit fel ea este inversă aceleia pe care am văzut-o în astronomie, unde se urmărește cognitiv o realitate și se ajunge la numărul incomensurabil. Toată chestiunea alunecă undeva în haos, prin însuși procesul de cunoaștere; în embriologie ne sustragem haosului. La un moment dat putem surprinde în anumite forme, asemănătoare formelor geometrice, ceea ce iese din haos. Într-o anumită măsură putem spune următoarele: În astronomie, prin procesul de cunoaștere intrăm, matematizând, în haos; și în observația simplă din embriologie avem haos, rezultă haos când observația nu mai este posibilă. Când observația devine posibilă ieșim din haos și intrăm în activitatea de geometrizare. Pentru unii biologi este un ideal chiar – și pe bună dreptate – a prinde sub formă geometrică ceea ce apare în embriologie. Acest ideal justificat nu este doar acela de a picta naturalist embrionul în devenire, ci de a-l construi conform unei legități interioare, asemănătoare legității din figurile geometrice.
În concluzie putem spune: Urmărind realitatea prin observație ieșim din ceva, care la început este tot atât de puțin apropiat [Nota 51] pentru cunoașterea noastră ca și numărul incomensurabil dincoace (în astronomie) [Nota 52]. Într-un anume fel noi am împins cunoașterea până la un punct în care nu mai putem avansa cu matematica; iar în embriologie ne-am început cunoașterea abia într-un punct unde putem interveni cu ceva asemănător cu geometria [Nota 53]. Vă rog, duceți gândul până la capăt. Puteți să faceți acest lucru, pentru că el este un gând metodologic, cu alte cuvinte își are realitatea în noi.
Când am ajuns cu calculul la un număr incomensurabil, adică la un punct unde nu mai putem să introducem realitatea concis, simplu, într-un număr, atunci investigația noastră trebuie să înceapă prin a vedea – și spre așa ceva ne vom îndrepta în conferințele următoare – dacă nu cumva și în privința formelor geometrice nu stăm la fel ca și cu structurile aritmetice sau analitice. Configurația analitică conduce la un număr incomensurabil. Să ne punem pentru început întrebarea: Cum înfățișează formele geometrice mișcările cerești? Această configurare nu ne conduce oare într-un punct asemănător celui la care ne conduce analiza, adică să fim nevoiți să ne lovim de numărul incomensurabil? Când urmărim corpurile cosmice, planetele, nu ajungem oare la o limită unde trebuie să spunem: Acum nu mai pot înfățișa forme geometrice, ceea ce văd nu mai poate fi cuprins în forme geometrice? La fel cum a trebuit să părăsim domeniul numerelor reale, putem fi nevoiți să părăsim și domeniul în care cuprindem realitatea cu ajutorul desenului, prin forme geometrice – chiar și aritmetice, algebrice, analitice – cum ar fi spiralele și așa mai departe; să ajungem în incomensurabil chiar pe cale geometrică. Oricum situația care urmează este cât se poate de ciudată. Vedeți dumneavoastră, analiza nu o putem aplica prea mult deocamdată în embriologie, dar geometria deja ne apare fantomatică acolo unde încercăm să dezvoltăm realitățile embriologice din haos. La capătul acestei cercetări nu apare într-atât un incomensurabil numeric, cât mai ales ceva care se plămădește într-o formă comensurabilă din ceva incomensurabil ca formă.
Am încercat aici să privim realitatea din două puncte de vedere polar-opuse: acela în care cunoașterea ne scoate din procesul de analiză și ne conduce la fenomenul incomensurabil și acela în care prin observație ieșim din haos și cuprindem realitatea în forme din ce în ce mai comensurabile. Acestea sunt lucrurile care trebuie evocate în primul rând și cu cea mai mare claritate în fața sufletului, dacă dorim neapărat să examinăm realist cele ce se întâmplă astăzi în știința exterioară.
La cele spuse aș vrea să mai adaug o prezentare metodologică, pentru ca mâine să putem intra într-un fapt ceva mai real. Aș vrea să adaug următoarele: tot ceea ce am prezentat până acum s-a bazat într-un fel pe ipoteza că întotdeauna ne-am apropiat de fenomenele din cosmos ca matematicieni. După aceea a reieșit faptul că la un moment dat matematicianul ajunge la un prag la care ajunge și în matematica formală. Dar la baza felului în care noi gândim există ceva ce probabil se observă cel mai puțin, pentru că se ascunde mereu sub masca evidenței, iar noi nu abordăm problema din unghiul cel mai potrivit. Acesta se referă în special la problema aplicării matematicii la realitate. Cum procedăm noi de fapt aici? Dezvoltăm matematica ca pe o știință formală – în deducțiile pe care le face ea ni se pare absolut sigură –, după care aplicăm matematica la realitate și nu ne gândim că de fapt o aplicăm folosind anumite supoziții sau ipoteze. Astăzi s-a creat chiar un curent de cercetare, pentru a vedea în ce măsură putem aplica matematica la realitatea exterioară, făcând doar anumite ipoteze. Această necesitate rezultă atunci când vrem să extindem matematica în afara anumitor limite. În această situație se pornește construind niște legi, care de data aceasta nu se obțin pe baza realității exterioare – așa cum am arătat mai înainte cu ocazia prezentării legilor lui Kepler –, ci pe baza procesului matematic însuși, legi care nu sunt de fapt altceva decât legi inductive, create pe bază matematică. Acestea se utilizează apoi deductiv, prin faptul că și acum se merge în continuare și se construiesc cu ajutorul lor teorii matematice foarte stufoase.
Astfel de legi sunt, de exemplu, cele de care se lovește oricine are de-a face cu matematica. Semnificativ pentru acest procedeu al cercetărilor matematice sunt cele indicate de către prietenul nostru Blümel [Nota 54], în conferințele ținute la Dornach. Una dintre legile despre care este vorba este în primul rând așa-numita lege a comutativității. Ea se poate exprima în felul următor: Este evident că:
a + b = b + a sau
a × b = b × a
Este de la sine înțeles, atâta timp cât ne aflăm în domeniul numerelor reale, dar cu toate acestea rămâne o lege inductivă, dedusă prin aplicarea postulatelor aritmeticii la numerele reale.
A doua lege este legea asociativității. Ea s-ar putea exprima în felul următor:
(a + b) + c = a + (b + c)
Și de data aceasta este vorba de o lege, care este dedusă pur și simplu din aplicarea postulatelor aritmetice la numerele reale.
A treia lege este așa-numita lege a distributivității. Ea s-ar putea exprima sub forma de mai jos:
a × (b + c) = ab + ac
Avem din nou o lege obținută pur și simplu inductiv, pe baza aplicării postulatelor aritmeticii la numerele reale.
Cea de-a patra lege poate fi formulată în următorii termeni: Produsul a două numere poate fi zero doar dacă unul dintre factori este egal cu zero. Această lege este și ea doar o lege inductivă, rezultată prin aplicarea postulatelor aritmeticii la numere reale. Avem deci aceste patru legi: legea comutativității, legea asociativității, legea distributivității și această lege a anulării produsului. Aceste legi se află deci la baza matematicii formale și cu ele se operează și în continuare. Ajungem aici, nu putem tăgădui, la lucruri extraordinar de interesante.
Problema care se pune acum este că aceste legi sunt valabile atât timp cât rămânem în domeniul numerelor reale și al postulatelor lor, însă niciodată nu se urmărește atent dacă realitatea corespunde cu acestea. Putem spune că în tipurile noastre de experiențe formale este valabilă legea a + b = b + a, dar este valabilă ea și în realitate? Nu avem nici o bază pentru a descoperi de ce trebuie să fie valabilă ea și în realitatea exterioară. Putem foarte bine să avem surpriza să nu găsim confirmarea așteptată atunci când spunem că într-un proces din realitatea exterioară este valabilă legea a + b = b + a. Dar chestiunea are o altă latură. În noi avem înclinația spre această legitate și de aceea ne apropiem de realitate cu această legitate; ceea ce nu corespunde acestei legități cade în afara observației noastre. Aceasta este cealaltă latură. Cu alte cuvinte, formulăm postulate pe care le aplicăm la realitate și le luăm drept axiome ale realității însăși. Noi nu ar trebui să spunem decât atât: observ un anumit domeniu al realității și după aceea observ cât de departe ajung cu afirmația a + b = b + a. Mai mult nu am voie să spun. Pe măsură ce mă apropii de realitate cu această afirmație voi găsi tot ceea ce îi corespunde, iar ceea ce nu îi corespunde voi da frumos la o parte. Aceeași deprindere o avem și în alte domenii. De exemplu, în fizica elementară spunem că corpurile au o proprietate de inerție și apoi definim în ce ar consta inerția, arătând că datorită ei corpurile nu își părăsesc poziția în care se află sau nu își modifică mișcarea fără un impuls din afară. Dar aceasta nu este o axiomă, ci un postulat [Nota 55]. Eu nu aș avea voie să spun decât următorul lucru: Un corp la care observ că starea lui de mișcare rămâne neschimbată îl numesc inerțial; și acum încep să caut în realitate ce corespunde acestui postulat. Deci, formându-mi anumite noțiuni, eu nu îmi formez de fapt decât niște linii directoare, pentru a putea să pătrund într-un anume fel realitatea cu aceste noțiuni, și trebuie să îmi las drumul deschis pentru a pătrunde alte realități cu alte noțiuni. Gândesc just cele patru teoreme de bază ale teoriei numerelor numai atunci când le privesc ca pe ceva care îmi dă o orientare; ca pe ceva care îmi dă posibilitatea de a pătrunde regulator, ordonator în realitate. Și sunt pe un drum greșit dacă iau matematica ca pe un element constitutiv al realității, căci aici realitatea s-ar putea să mă contrazică în anumite domenii. Iar o astfel de contrazicere este aceea despre care am vorbit, și anume că la analizarea fenomenelor cerești intervine incomensurabilitatea.