Am ajuns cu discuția noastră la un punct, de la care trebuie mers cu extraordinar de mare precauție mai departe, pentru a vedea clar în ce măsură se menține pericolul de a ieși cu reprezentările din realitate, sau de a rămâne în cadrul reprezentărilor reale, adică de a scăpa de pericol.
Este vorba desigur de faptul că ultima oară am prezentat, oarecum ca un postulat, propunerea de a compara simplu două fapte: apariția în cadrul sistemului planetar a fenomenelor cometare și – în cele din urmă tot în cadrul sistemului planetar, chiar dacă legat altfel de acesta – ceea ce observăm în fenomenele de fecundare. Pentru a avea însă aici reprezentări cât de cât justificate, mai întâi trebuie văzut dacă chiar este posibil să se caute analogii între două lucruri aparent atât de îndepărtate în lumea exterioară reală. Nu vom ajunge la nici un rezultat din punct de vedere metodologic, dacă nu vom putea indica un loc unde să existe ceva asemănător, care să ne poată conduce apoi mai departe în modalitatea de a privi lucrurile.
Am văzut cum trebuie pe de o parte să aplicăm elementul figurativ, de formă, matematicul, cum însă suntem obligați să cuprindem mereu într-un fel oarecare calitativul, să ne apropiem de calitativ. Tocmai de aceea astăzi vom introduce ceva cu privire la om, ceva ce rezultă atunci când privim acest om, care în cele din urmă este o imagine, după cum putem remarca din fiecare detaliu al acestor conferințe o imagine a fenomenelor cerești, pe care trebuie să le determinăm. Fiindcă omul este acest ceva, trebuie mai întâi să facem lumină în ceea ce îl privește chiar pe el. Va trebui să înțelegem într-o măsură imaginea de la care vrem să plecăm, să înțelegem perspectiva interioară. Așa cum la o pictură – pentru a putea face trecerea de la tablou la raporturile spațiale, pentru a raporta deci imaginea la realitatea sa – trebuie mai întâi lămurit ce semnifică o scurtare de perspectivă sau ceva asemănător, tot așa, dacă vrem să abordăm realitatea din univers pornind de la om, trebuie mai întâi să facem lumină în privința omului. Este însă extrem de greu să te apropii cu niște reprezentări palpabile de om, tu însuți fiind om. De aceea astăzi aș dori să vă aduc în fața sufletelor, prin relații foarte simple, reprezentări palpabil-impalpabile, reprezentări pe care probabil majoritatea dintre dumneavoastră le cunosc bine de mult timp, dar pe care totuși trebuie să le punem în fața sufletului într-un anumit context, pentru ca pe baza acestor reprezentări – ce pe de o parte se pot sesiza aparent ușor, pe de altă parte însă, în anumite limite, par de necuprins – să ne putem orienta când este vorba să înțelegem lumea exterioară.
Poate părea forțat să accentuăm mereu faptul că, dacă vrem să înțelegem fenomenele cerești, trebuie să revenim la viața de reprezentare a omului. Este clar totuși că în fenomenele cerești, chiar dacă le descriem încă cu mare precauție, nu avem altceva decât un fel de imagini optice, saturate cu tot felul de reprezentări matematice. Chiar ceea ce ne oferă astronomia are caracterul fundamental de imagine pură. De aceea, dacă vrem să reușim, trebuie să cercetăm cum se formează imaginea în om, în caz contrar nu vom putea dobândi o poziție corectă față de ceea ce ne poate spune astronomia. Iar astăzi aș dori să pornesc de la o chestiune matematică extrem de simplă, pentru a vă arăta că și în matematica propriu-zisă, într-un alt domeniu decât cel în care am fost conduși prin rapoartele perioadelor de revoluție ale planetelor, apare ceva impalpabil. Acest lucru ne întâmpină dacă privim curbele uzuale într-o anumită legătură [Nota 111]. Mulți dintre dumneavoastră cunosc deja chestiunea, astăzi vreau doar să o prezint dintr-un punct de vedere mai deosebit.
Dacă privim curba pe care dumneavoastră o cunoașteți sub denumirea de elipsă, cu cele două focare A și B ale ei, știți desigur că elipsa este caracterizată prin aceea că suma a + b a distanțelor de la un punct oarecare M al elipsei la cele două focare rămâne mereu constantă. Aceasta este caracteristica elipsei, faptul că suma distanțelor de la un punct oarecare al ei la două puncte fixe, cele două focare, rămâne constantă (vezi fig. 1).
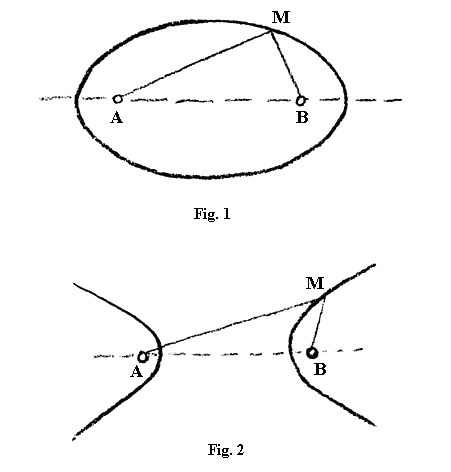
Avem apoi a doua curbă, hiperbola (vezi fig. 2). Știți că ea are două ramuri și că este caracterizată prin aceea că diferența a − b a distanțelor de la un punct oarecare al ei la cele două focare este o mărime constantă. Elipsa ar fi deci curba sumei constante, iar hiperbola curba diferenței constante, după care urmează să ne întrebăm: Care este curba produsului constant?
Am atras deseori atenția că această curbă a produsului constant este așa-numita curbă a lui Cassini [Nota 112] (vezi fig. 3).
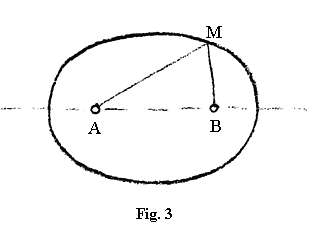
Să privim chestiunea în felul care urmează: avem două puncte A și B și urmărim comportarea unui punct oarecare în raport cu distanțele sale față de A și B. Avem deci o distanță AM, cealaltă distanță BM și punem condiția ca aceste două distanțe înmulțite să dea o mărime constantă. Această mărime constantă o voi nota, pentru a simplifica calculul, b2, iar distanța AB o voi nota cu 2a. Dacă la mijlocul distanței dintre A și B considerăm un punct (O) ca centru al unui sistem de coordonate și calculăm pentru fiecare punct care îndeplinește condiția de mai sus ordonata – dacă deci punem aici punctul să înconjoare centrul de coordonate astfel încât în oricare punct al acestei curbe AM × BM = b2 – atunci pentru ordonata unui punct oarecare, pe care o numim y, obținem ecuația care urmează – vă voi comunica doar rezultatul, din simplul motiv că fiecare își poate procura foarte ușor modul de calcul. El se găsește în orice manual de matematică care tratează aceste lucruri. Pentru y obținem valoarea:
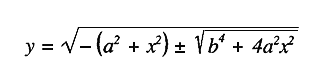
Dacă ținem cont că aici (înaintea rădăcinii pătrate de dedesubt) nu avem nevoie neapărat de semnul minus, deoarece prin aceasta am obține un y imaginar, deci dacă luăm în considerare doar semnul plus, atunci obținem următoarele:
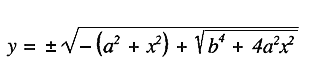
Dacă trasăm după aceea curba corespunzătoare, vom obține o linie asemănătoare unei elipse, fără însă să coincidă cu aceasta, numită – după cel care a descoperit-o întâi – curba lui Cassini. Ea
este simetrică dreapta-stânga față de axa ordonatei și simetrică sus jos față de abscisă. Acesta este un lucru pe care trebuie să îl reținem. Un fapt caracteristic pentru ea, cel puțin în ceea
ce ne privește, este că această curbă are diferite forme. Ea are forme diferite după cum b, pe care l-am amintit mai sus, este mai mare decât a, egal cu a sau mai mic
decât a. Curba pe care am desenat-o puțin mai devreme ia forma respectivă dacă b > a și totodată dacă mai este îndeplinită condiția ca b să fie mai mare sau egal cu 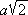 . De exemplu, dacă
. De exemplu, dacă 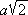 , sus și
jos avem o curbură clară. Dacă
, sus și
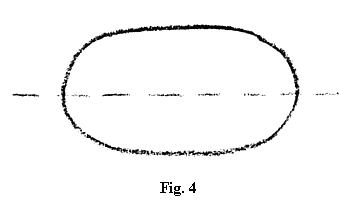
jos avem o curbură clară. Dacă 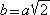 , atunci sus și jos curba se transformă în dreaptă, se aplatizează, în așa fel
încât sus și jos ea devine aproape o dreaptă (fig. 4).
, atunci sus și jos curba se transformă în dreaptă, se aplatizează, în așa fel
încât sus și jos ea devine aproape o dreaptă (fig. 4).
Dacă însă se ajunge ca 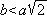 , întreaga conformație a curbei se schimbă. Ea capătă forma din figura 5. Iar dacă b
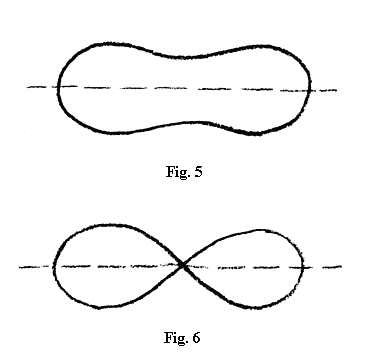
= a curba ia o formă cu totul specială, ca în figura 6. Ea se întoarce oarecum în sine, se intersectează pe ea însăși și apoi se regăsește din nou, realizând forma specială de lemniscată.
Lemniscata este, așadar, o formă specială a curbei lui Cassini. Forma specială este generată datorită raportului existent între mărimile constante care apar în ecuația sau caracteristica curbei.
În ecuație avem doar aceste mărimi constante b și a, iar forma curbei depinde de raportul dintre aceste două mărimi.
, întreaga conformație a curbei se schimbă. Ea capătă forma din figura 5. Iar dacă b
= a curba ia o formă cu totul specială, ca în figura 6. Ea se întoarce oarecum în sine, se intersectează pe ea însăși și apoi se regăsește din nou, realizând forma specială de lemniscată.
Lemniscata este, așadar, o formă specială a curbei lui Cassini. Forma specială este generată datorită raportului existent între mărimile constante care apar în ecuația sau caracteristica curbei.
În ecuație avem doar aceste mărimi constante b și a, iar forma curbei depinde de raportul dintre aceste două mărimi.
Mai este posibilă acum și o a treia situație, aceea când b < a. Și în acest caz se obțin valori pentru curbă. Chiar dacă b este mai mic decât a, ecuația se poate rezolva și obținem valori, ordonate și abscise, pentru curbă, însă aceasta continuă să se comporte deosebit. Căci dacă b < a, obținem două ramuri de curbă, care se prezintă aproximativ ca în figura 7.
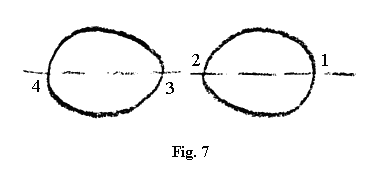
Obținem o curbă discontinuă. Aici ne aflăm exact în punctul în care în matematică ne întâmpină, într-un fel, palpabil-impalpabilul, adică ceva ce se poate sesiza greu în spațiu. În sensul ecuațiilor matematice, acestea nu sunt două curbe, ci o curbă, o singură curbă, exact ca cele din figurile 3–5. În ceea ce privește lemniscata, chestiunea mai este încă în tranziție. Aici punctul pe care îl descrie curba coboară, traversează drumul pe care l-a parcurs mai înainte și din nou revine de unde a plecat. În ceea ce privește figura 7, trebuie să ne imaginăm următoarele: dacă punctul M începe să se deplaseze pe această curbă, el nu traversează aici simplu traiectoria în partea cealaltă, ci parcurge drumul exact ca în cazul lemniscatei, descrie o curbă și apoi ajunge din nou de unde a plecat. Așadar, vedeți că suportul punctului de-a lungul acestor curbe dispare în mijloc. Dacă vreți să înțelegeți curba, nu puteți să vă imaginați decât că aici în mijloc aceasta dispare. Dacă încercați să vă formați o reprezentare care să rămână continuă pe tot parcursul procesului de reprezentare, ce va trebui să faceți? O astfel de curbă (primele trei forme), nu-i așa, este ușor să v-o imaginați – spun asta doar în paranteză, pentru filistinii obișnuiți. Puteți să vă reprezentați mereu un punct, fără să ajungeți în situația ca reprezentarea să se rupă brusc. În cazul lemniscatei va trebui să modificați într-adevăr procedeul comod de a merge simplu de jur împrejur. Aici încă mai merge, puteți să vă mențineți procesul de reprezentare. Mai departe însă, dacă ajungeți la forma cu două ramuri, care nu este o curbă filistină, dacă vreți să v-o reprezentați va trebui, pentru a rămâne în acea reprezentare continuă, să spuneți: Spațiul nu-mi mai oferă pentru asta nici un punct de sprijin. Când avansez pe această porțiune (de la 1 la 2) [Nota 113] trebuie, dacă vreau să nu îmi întrerup activitatea de reprezentare și să privesc cealaltă ramură ca pe ceva izolat în sine [Nota 114], să ies cu reprezentarea din cadrul spațial (porțiunea de la 3 până la 4), nu mai pot rămâne în spațiu. Vedeți așadar că însăși matematica ne oferă exemple care ne aduc în situația să ieșim din spațiu, dacă vrem să rămânem în reprezentarea continuă. Realitatea este astfel întocmită, încât ne pretinde să ieșim cu reprezentarea noastră din spațiu. Deci chiar aici, în cadrul matematicii, ne apare ceva prin care se vede că trebuie să părăsim spațiul, dacă vrem să ajungem să ne reprezentăm ceva. În tot ceea ce am realizat noi înșine prin reprezentare, prin faptul că am început să gândim, suntem obligați să recunoaștem că spațiul nu ne mai ajută în continuare. În caz contrar, nu putem ține cont în ecuație de toate variantele posibile.
Așadar, atunci când parcurgem un proces de reprezentare asemănător, întâlnim mai multe lucruri de felul acesta. As vrea să-l amintesc doar pe cel mai la îndemână, pe care îl întâlniți atunci când vă puneți următoarea problemă: elipsa este deci locul geometric al sumei constante, ea se caracterizează prin aceea că este curba de sumă constantă. Hiperbola este curba de diferență constantă. Curba lui Cassini cu diferitele ei forme este curba produsului constant. Dacă avem două puncte, A și B, și în altă parte un punct M și formăm un cât, împărțind BM la AM, trebuie deci să existe și o curbă de împărțire constantă. Va trebui să găsim puncte M1, M2, și așa mai departe, pentru care întotdeauna rapoartele sunt egale între ele și egale cu un anumit număr constant. Această curbă este chiar cercul.
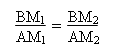 etc.
etc.Dacă căutăm punctele M1 și M2 obținem un cerc, care se află în acest raport față de punctele A și B (vezi fig. 8). În felul acesta putem să spunem: Pe lângă definiția cercului, care este o definiție comună – și anume că cercul este locul geometric al punctelor aflate la distanță egală de un punct fix –, mai există și o altă definiție a cercului: cercul este acea curbă pentru care fiecare punct al ei îndeplinește condiția că raportul distanțelor de la acest punct la două puncte fixe este același.
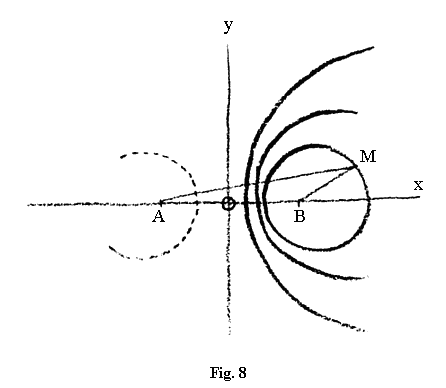
Acum, avem posibilitatea să observăm și altceva, pentru că, vedeți dumneavoastră, dacă BM : AM îl exprimăm prin m : n, deci
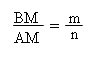
în ecuație obținem mereu valori corespunzătoare, putem găsi cercul undeva. Făcând deci aceasta obținem forme diferite ale cercului [Nota 115], după mărimea raportului m față de n: dacă n este mult mai mare decât m, obținem un cerc puternic curbat; dacă n se micșorează obținem un cerc mai puțin curbat (fig. 8, dreapta). Astfel, cercul devine cu atât mai mare cu cât diferența dintre m și n scade. Treptat, dacă urmărim acest raport în continuare, vedem că cercul ia forma unei drepte. Puteți urmări aceasta în ecuație [Nota 116]. Cercul devine însăși axa ordonatelor. Când m = n, deci când raportul m : n devine egal cu 1, cercul se transformă în axa ordonatelor. În acest fel cercul se transformă într-o dreaptă, axa ordonatelor.
Nu trebuie să vi se pară prea curios că se întâmplă așa. Este desigur un lucru pe care ți-l poți imagina. Chestiunea însă se prezintă altfel dacă vrem să mergem mai departe, spunându-ne că cercul, care se aplatizează din ce în ce mai mult, devine dreaptă prin aplatizare din interior. Cercul se transformă astfel tocmai pentru că raportul constant din ecuație suferă o modificare. Acest raport constant poate crește, desigur, în continuare peste 1, astfel că arcurile de cerc apar în stânga axei y; dar cum trebuie să ne reprezentăm acum acest cerc? Trebuie să facem un lucru cu totul special, și anume trebuie să ne imaginăm un cerc care nu este curbat spre înăuntru, ci este curbat spre afară. Desigur că nu am cum să desenez acest cerc [Nota 117], dar trebuie să ne imaginăm un cerc care este curbat spre exterior. În cazul cercului obișnuit, curbura este spre interior (cercul a din fig. 9, partea hașurată). Dacă urmărim drumul lui, acesta se închide. Dacă alegem în mod corespunzător constanta din ecuație vom obține o dreaptă. Din nou curbura acesteia este aici (în dreapta ordonatei, partea hașurată), însă această curbură este mai greu de interpretat decât cealaltă curbură, care peste tot tinde spre centrul cercului. Această curbură (cazul dreptei) ne face să ne gândim că centrul se află undeva la depărtare infinită, cum se spune. Acum însă, în cazul cercului din stânga dreptei, mergem cu gândul la un cerc curbat în exterior. Curbura acestuia nu este deci înspre partea nehașurată a cercului b, acesta ar fi cercul filistin, ci înspre partea hașurată a acestuia; și exact din același motiv, în partea nehașurată nu avem interiorul cercului, ci exteriorul lui, iar în partea hașurată avem interiorul cercului.
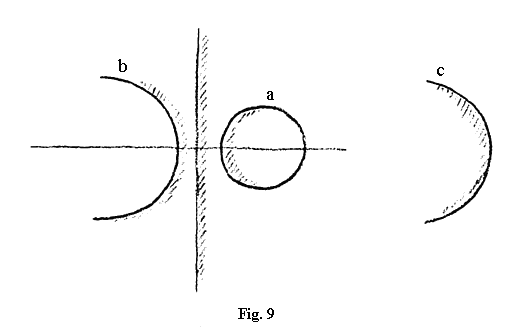
Și acum vă rog să comparați aceasta cu ceea ce v-am spus până acum: curba lui Cassini cu variantele sale, lemniscata și forma cu două ramuri. Am prezentat cercul (a) de curbură obișnuită, interiorul fiind în partea hașurată și exteriorul în partea nehașurată. Mai avem și o a doua formă de cerc (b) – acum nu putem indica decât cercul – unde curbura este în exterior, interiorul fiind partea hașurată și exteriorul partea nehașurată. Prima formă de cerc, (a), dacă o comparăm cu curba lui Cassini, ar corespunde formelor închise, mergând până la lemniscată. Și avem un al doilea cerc (b), care trebuie imaginat conform figurii din stânga, având curbura spre exterior, și în partea cealaltă exteriorul. Vedeți, realitatea este astfel încât, dacă avem de-a face cu produsul, obținem forme ale curbei lui Cassini în care, după ce suntem proiectați afară din spațiu, putem trasa iarăși cealaltă ramură a curbei, pe partea cealaltă. Ea revine din nou în spațiu. Dar pentru a trece de la o ramură la cealaltă, suntem întâi aruncați afară din spațiu. În cazul cercului, lucrurile devin ceva mai complicate. Cu siguranță și aici, la trecerea de la cerc la dreaptă, suntem proiectați în afara spațiului, dar acum în nici un caz nu mai putem desena ceva închis. Acest lucru nu este posibil. Când trecem de la curba produsului constant la curba câtului constant, încă mai putem urmări gândul spațial.
Este extraordinar de important să ne ocupăm cu formarea de reprezentări care, aș spune eu, încă se mai strecoară în astfel de forme de curbă. Sunt convins că toți aceia care se îndeletnicesc cu matematica întâlnesc astfel de discontinuități, dar după aceea se lenevesc în a-și mai reprezenta ceva și se opresc la acele formule, fără să mai încerce să treacă la ceea ce ar trebui să le însoțească, o reprezentare efectiv continuă. Până acum niciodată nu am văzut ca în tratarea disciplinelor matematice să se pună un accent prea mare pe formarea unor astfel de reprezentări. Nu știu acum, întreb pe matematicienii aici de față, domnul Blümel, domnul Baravalle [Nota 118], dacă lucrurile nu stau altfel în învățământul superior, dacă acolo nu se acordă cumva o valoare mai mare acestor lucruri? (Domnul Carl Unger [Nota 119] atrage atenția asupra imaginilor cinematografice.) Da, aceasta este o pseudoprocedură, când vrei să o faci cumva în cadrul spațiului empiric, deci prin intermediul acestor cinematografe sau ceva de genul acesta. Va trebui în acest caz să introduci o „iuțeală de mână”. Nu este posibil să realizezi în spațiul empiric o reprezentare adecvată, trebuie să introduci o șmecherie.
Problema care se pune acum este dacă undeva în realitate există ceva care ne obligă să vedem ceva real în aceste curbe. Aceasta este întrebarea pe care aș dori să o pun. Dar, în plus, înainte chiar de a trece la caracterizarea acelui lucru care i-ar putea corespunde în realitate, aș dori să adaug ceva, care probabil ar putea să vă faciliteze trecerea de la aceste reprezentări abstracte la realitate. Voi explica aceasta în cele ce urmează. În astronomia teoretică, în fizica teoretică puteți pune și o altă problemă. De exemplu, puteți pune următoarea problemă: Să presupunem că aici (fig. 10) avem o sursă de lumină A, care sursă de lumină luminează un punct M.
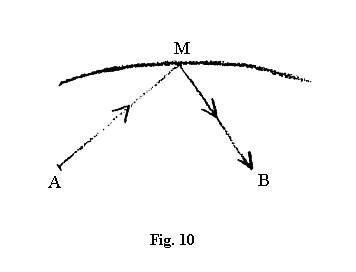
Intensitatea cu care strălucește acest punct M este observată din punctul B. Deci din punctul B se observă, să zicem, cu niște instrumente optice corespunzătoare, strălucirea punctului M, care este luminat din A. Sigur că, funcție de depărtarea punctului B față de M, noi vom vedea diferit intensitatea acestei străluciri. Dar există un drum pe care îl poate descrie acest punct M, astfel încât, primind lumina din A, el să lumineze în B mereu cu aceiași intensitate. Există un astfel de drum. Putem deci să punem următoarea întrebare: Care trebuie să fie traseul unui punct luminat dintr-un punct fix A, pentru ca în alt punct fix B el să aibă mereu aceeași strălucire? [Nota 120] Această curbă, după care se deplasează un astfel de punct, este curba lui Cassini. Din acest exemplu se vede că aici ceva care se află deja dincolo, în domeniul calitativului, se plasează într-un raport spațial, într-o curbă complicată. Calitatea, pe care trebuie o vedem deja în strălucirea luminoasă, în intensitatea strălucirii, această calitate devine aici dependentă de elementul figural din raporturile spațiale.
Am citat toate acestea doar pentru ca dumneavoastră să vedeți că există, fără îndoială, o anumită cale, care conduce de la ceea ce se exprimă figural-geometric la aspectul calitativ. Dar dintr-un anumit punct de vedere această cale este totuși departe. Și acum să trecem la ceva care, pentru a-l putea prezenta în amănunțime, ar necesita desigur luni de zile, dar pe care totuși vreau să îl mentionez. Totodată dumneavoastră trebuie să țineți seama îndeosebi de faptul că eu nu vreau să indic decât niște linii orientative, a căror dezvoltare ulterioară, respectiv dezvoltarea aspectelor prin care puteți să găsiți întotdeauna confirmarea, este lăsată în seama dumneavoastră; fiindcă, vedeți dumneavoastră, ceea ce trebuie să intervină ca o relație între știința spiritului și știința empirică actuală este o muncă foarte vastă, o muncă enorm de vastă. Dar odată liniile directoare stabilite, se poate, într-un anume fel, efectua și această muncă. Este posibil. Trebuie însă să te implici într-un mod cu totul special în fenomenele empirice.
Dacă privim problema dintr-un cu totul alt unghi – aici am încercat, într-o anumită măsură, s-o privim dinspre latura matematică –, cuiva, care se preocupă cu organizarea corporală a omului, nu-i poate scăpa totuși ceva ce s-a scos adesea în relief în cadrul cercului nostru și asupra căruia s-a insistat sub cele mai diverse aspecte în convorbirile care s-au purtat pe marginea cursului pentru medici [Nota 121] ținut la Dornach în primăvara lui 1920. Nu-i poate scăpa faptul că între organizarea-cap și restul organizării omenești, de exemplu aceea a metabolismului, există anumite raporturi. Între ceea ce se desfășoară în cel de-al treilea sistem al omului, sistemul metabolic cu organele sale, și ceea ce se petrece în interiorul capului există o legătură nedefinită. Acest raport existent aici însă este greu de sesizat. Pe cât de clar apare, de exemplu, faptul că prin anumite îmbolnăviri sunt provocate deformații ale capului, ale craniului și alte lucruri asemănătoare, pe cât de clar deci se pot urmări biologic aceste lucruri de către cineva care le gândește rațional, pe atât de greu este să le cuprinzi într-o reprezentare. În mod obișnuit oamenii se mărginesc a spune: Trebuie să existe o legătură între ceea ce se petrece în cap și ceea ce se petrece în restul organizării omenești. Este un lucru greu de reprezentat tocmai din cauză că omului îi vine foarte greu să treacă de la cantitativ la calitativ. Dacă nu ne educăm, printr-o metodologie spiritual-științifică, să găsim totuși această cale de tranziție și să extindem și la calitativ aproximativ același fel de reprezentare utilizat în domeniul cantitativului, indiferent de ceea ce îi oferă omului experiența exterioară, dacă nu ne vom educa metodologic în această direcție, atunci întotdeauna se va ridica pentru înțelegerea noastră granița aparentă a fenomenelor exterioare.
Mai vreau să vă dezvălui un singur lucru, și anume cum vă puteți educa să gândiți metodologic calitativul într-un mod asemănător cu cantitativul. Tuturor vă este bine cunoscut fenomenul obișnuit al spectrului solar, al spectrului continuu, obișnuit. Știți că acolo se merge de la culoarea roșu la culoarea violet. Și știți desigur cu toții că Goethe s-a luptat să arate că acest spectru, într-un anumit sens, este inversul spectrului care ia naștere atunci când privești întunericul prin prismă la fel cum privești luminosul prin prismă. Se obține atunci un fel de spectru inversat, pe care Goethe l-a ordonat de asemenea [Nota 122]. În spectrul obișnuit, nu-i așa, avem verdele, într-o direcție mergând spre violet și în partea cealaltă mergând spre roșu (fig. 11); în cazul spectrului pe care îl obține Goethe când așază o bandă neagră (pe care o privește prin prismă – n.t.), în care avem culoarea florii de piersic de o parte roșul și de partea cealaltă violetul (fig. 12).
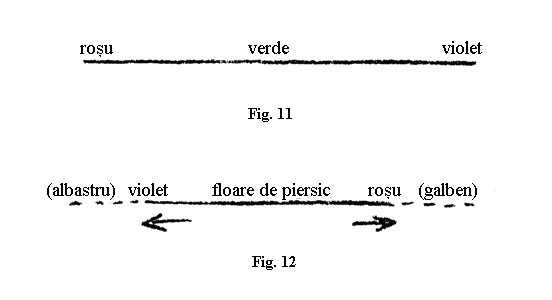
Obținem într-un fel două benzi de culoare, opuse la mijloc una față de cealaltă, calitativ opuse, ambele evoluând inițial pentru noi, s-ar putea spune, spre infinit. Dar putem să gândim la început simplu că axa longitudinală a spectrului obișnuit nu este o dreaptă simplă, ci un cerc, așa cum orice dreaptă este un cerc. Dacă această dreaptă este un cerc, atunci ea se reîntoarce la sine și noi putem foarte bine să privim acest punct, în care apare floarea de piersic, ca celălalt punct, în care se întâlnesc violetul, care merge spre dreapta, și roșul, care merge spre stânga. Ele se ating stânga și dreapta – la infinit, desigur. Dacă însă ne-ar reuși – nu știu dacă dumneavoastră știți că exact în această direcție în institutul nostru de fizică urmează să fie făcut unul din primele montaje experimentale [Nota 123] – să curbăm într-un fel spectrul în sine, atunci și aceia care nu vor să înțeleagă această chestiune doar mental vor vedea, de asemenea, că și aici avem de-a face cu calitativul. Astfel de reprezentări sunt reprezentările-limită din matematică, unde, ca și în geometria sintetică, suntem nevoiți să considerăm dreapta, chiar din punct de vedere strict obiectiv, ca pe un cerc; unde suntem nevoiți să admitem pentru o dreaptă doar un punct infinit-depărtat; unde suntem nevoiți să admitem ca limită a unui plan o singură dreaptă și nu o linie sus și una jos; unde suntem nevoiți să ne imaginăm marginile spațiului infinit nu ca pe o sferă sau așa ceva, ci ca pe un plan. Dar dacă nu vrem să privim decât realitatea empirică, senzorială, atunci și aceste reprezentări devin într-un anumit fel reprezentări-limită ale realității senzorial-empirice.
Asta ne conduce acum la ceva care altminteri ar rămâne mereu confuz. Tocmai am menționat acest lucru. Ne conduce să gândim metodic acele reprezentări ce ar putea fi obținute atunci când lăsăm să se transforme forma de lemniscată a curbelor lui Cassini în forma cu două ramuri, acea formă cu două ramuri prin care suntem nevoiți să ieșim din spațiu și să comparăm aceste reprezentări cu ceea ce ni se oferă în realitatea empirică. De altfel, dumneavoastră faceți în mod curent acest lucru atunci când aplicați matematica la realitatea empirică. Ceea ce aveți dat în triunghi, numiți triunghi fiindcă mai întâi v-ați construit triunghiul în mod matematic. Ceea ce este dezvoltat interior în dumneavoastră sub aspect constructiv, îl aplicați la forma exterioară. Procedeul pe care îl indic eu aici este ceva mai complicat, însă este același procedeu ca atunci când gândiți cele două ramuri ale curbei duble a lui Cassini ca fiind o singură curbă. Dacă aplicati această reprezentare la ceea ce corespunde în capul omului funcțiunilor restului organismului, va trebui să vă imaginați că în cap există o dependență de restul organismului exprimabilă printr-o relație de același tip cu cea de mai sus, care însă cere o curbă discontinuă. Nu veți putea urmări asta printr-o metodă anatomică. Dacă vreți să urmăriți ce se exprimă în cap legat de ce se exprimă în organismul metabolic, trebuie să ieșiți din ceea ce împresoară fizic corpul. Va trebui deci să urmăriți organismul omenesc prin reprezentări care nu se obțin punând în locul fiecărui element al acestei reprezentări un altul senzorial-empiric adecvat. Dacă vrem să găsim această legătură din om, trebuie să ieșim din senzorial-empiric și să intrăm în ceva de altă natură.
Este cât se poate de instructiv să urmărim metodologic aceasta în continuare, să procedăm efectiv la o astfel de examinare. Căci, de fapt, organizarea omenească rezidă în ceva care nu se poate cuprinde doar anatomizând. Exact așa cum prin curba lui Cassini suntem expediați afară din spațiu, tot așa atunci când examinăm omul suntem alungați, prin însuși modul de examinare, în afara corpului. Mai întâi trebuie să ne reprezentăm că, pentru a evalua omul în ansamblu, suntem alungați din tot ceea ce poate fi sesizat fizic-empiric la om. Nu comitem nici un fel de păcat împotriva spiritului științific menționând aceste lucruri. Ele sunt foarte departe de toate acele ipoteze care se emit și care adesea nu sunt decât pure fantezii despre fenomenele naturii; căci aceste lucruri se referă într-adevăr la întregul mod în care este situat omul în lume. Iar dumneavoastră nu veți umbla după ceva ce nu există, ci după ceva identic cu ceea ce se exprimă în raportul omului care matematizează față de realitatea empirică.
Nu se pune absolut deloc problema să căutăm tot felul de ipoteze nejustificate, ci vrem doar, întrucât realitatea este evident complicată, să căutăm și alte raporturi de cunoaștere față de realitatea interioară decât acela simplu, al omului care matematizează față de realitatea fizic-empirică. Iar dacă o dată ați deschis ochii asupra acestor lucruri, veți fi conduși să cercetați și dacă ceea ce se întâmplă în exteriorul omului, în alte domenii decât cel astronomic, de exemplu în cadrul fenomenelor pe care noi le numim chimice, fizice etc., dacă aceleași fenomene, pe care afară le considerăm chimice, se petrec la fel și în om, în interiorul omului viu, dacă nu cumva ele mai necesită aici o transcendere, care conduce cumva în afara spațiului.
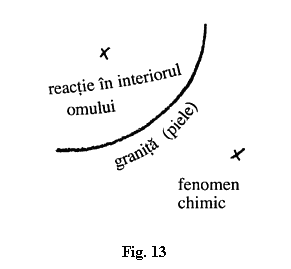
Analizați acum întrebarea importantă care decurge de aici. Să zicem că am avea un fenomen chimic oarecare și granița față de interiorul omului (fig. 13). Dacă acest fenomen chimic ar putea provoca un altul, astfel încât omul să reacționeze în interior, atunci, dacă ră¬ânem în domeniul empiric, bineînțeles că spațiul ar fi mijlocitorul. Dacă însă acest fenomen se continuă în om, în sensul că prin alimente el se hrănește și procesele se continuă în interior, atunci întrebarea care se pune este: Ceea ce acționează aici ca forță în fenomenul chimic rămâne, când se continuă în om, în același spațiu în care se desfășura afară? Sau poate trebuie să ieșim din spațiu? Și aici aveți analogia cu cercul care se transformă în linie dreaptă. Și dacă veți căuta cealaltă formă a sa, unde ceea ce de obicei este orientat în afară apare îndreptat spre interior, ați ieșit complet în afara spațiului.
Întrebarea care se pune observând procesele ce se întâmplă în exterior, în afara omului, și continuarea evoluției lor în interiorul lui este dacă nu avem nevoie de niște reprezentări care, pentru a avea continuitate, să trebuiască să iasă complet din spațiu. Singura obiecție ce se poate aduce împotriva acestor lucruri este că, ce-i drept, ele solicită mai mult capacitatea umană decât acelea cu care ne apropiem astăzi de fenomene, motiv pentru care ele și sunt puțin agreate în învățământul superior. Ele sunt foarte incomode fiindcă de fapt aici ar trebui să se ceară ca omul, înainte să se apropie de astfel de fenomene, să dobândească ceva care să-l facă apt să sesizeze aceste fenomene. Nicăieri astăzi, în activitatea noastră de predare, nu există ceva asemănător, dar va trebui introdus neapărat, altfel o să ajungem să vorbim despre un fenomen într-o totală incoerență, fără să mai vedem vreun pic realitatea. Căci încercați să reflectați puțin ce se întâmplă dacă cineva care observă cum se curbează cercul pe partea din interior (fig. 9, a) și cum se curbează pe partea cealaltă (b) rămâne un filistin și nu acceptă absolut deloc că în figura 9, b cercul se curbează pe partea hașurată. El spune: Nu există ca cercul să se curbeze în acest fel, curbura trebuie să o pun în interior (cercul c în loc de b), trebuie să mă așez, simplu, de cealăltă parte. În acest caz el vorbește aparent despre același lucru, dar își schimbă locul de observație.
Astăzi, când se descrie interior omul, se procedează de fapt la fel ca și atunci când descriem natura exterioară. Se spune: Ceea ce se află înăuntrul omului nu există absolut deloc, ci eu mă postez înăuntrul omului și spun: Curbura este îndreptată ca în fugura c. Eu privesc deci interiorul fără să țin seamă că pentru mine curbura s-a inversat. Fac din ceea ce există în interiorul omului o natură exterioară. Continui această natură exterioară pur și simplu dincolo de piele. Mă sucesc pe mine fiindcă nu vreau să merg împreună cu linia curbă, altfel arcuită decât înainte, după care teoretizez. Aceasta este de fapt acrobația care se realizează astăzi, care se realizează doar pentru a menține niște reprezentări comode. Nu vrem să urmăm îndeaproape realitatea, și pentru că nu dorim acest lucru ne sucim pe noi înșine; în loc să privim omul din față – e vorba acum de o comparație – privim natura din spate, ajungând astfel la diverse teorii despre om.
Vom încerca să continuăm acest subiect mâine.