Astăzi aș încerca să transpun în reprezentări câteva aspecte care ridică greutăți în înțelegerea lucrurilor pe care le-am analizat până acum, reprezentări care să vă arate cum, în practică, nu putem ajunge să înțelegem fenomenele cosmice cu ajutorul a ceea ce s-ar dori atât de mult să fie pus la baza acestei înțelegeri, conform comodității ce caracterizează obișnuințele omenești de gândire. Am analizat fenomenele cosmice în strânsă legătură cu omul, din unghiurile cele mai diferite. De exemplu, am indicat în repetate rânduri cum între forma umană și ceea ce ne întâmpină în fenomenele cerești se vădește o anumită legătură, indiferent dacă tabloul pe care îl concepem despre mișcările corpurilor cerești corespunde unui sistem cosmic mai vechi sau teoriilor copernicane. Tabloul trebuie raportat mereu, în felurite moduri, la om, am văzut acest lucru, și în nici o știință adevărată nu putem să nu acceptăm acest raport.
Acum intervin însă dificultăți considerabile. De-a lungul acestor conferințe am indicat mai întâi o anumită dificultate, care se exprimă în faptul că, atunci când se încearcă să se studieze rapoartele perioadelor de revoluție ale planetelor din sistemul nostru solar, rezultă numere incomensurabile, că deci este necesar cumva să ne oprim să mai calculăm; căci acolo unde intervin numere incomensurabile nu mai există o unitate (și unitate de măsură – n.t.) ușor de sesizat. Și astfel vedem că nu putem spera să ajungem vreodată să ne explicăm fenomenele cosmice cu ajutorul acelui mod matematic de a gândi și cu metodica de a sintetiza fenomenele din spațiul cosmic prin care chiar fenomenele sunt alungate din realitate, deci cu acele ipoteze pe care noi le punem la baza geometriei din spațiul tridimensional rigid obișnuit. Chiar ieri ne-a apărut o dificultate deosebită: am fost siliți să presupunem existența unui raport între Soare, Lună și Pământ, care sub o anumită formă trebuie să se exprime și în alcătuirea omului. Iar în clipa în care intervine acțiunea simultană a unei triade, în calculul spațial apar niște dificultăți considerabile. Asupra tuturor acestor lucruri v-am atras atenția. Acum poate apărea ceva care să ne permită, cel puțin ca un punct de sprijin, să ne formăm o reprezentare geometrică – dar geometrică într-o măsură mai ridicată – a ceea ce altfel ridică mari dificultăti atunci când se încearcă să se înțeleagă legăturile dintre fenomenele cerești prin calculul spațial.
Dacă ne întoarcem încă o dată la încercările, pe care vi le-am prezentat, de a înțelege cu adevărat alcătuirea omului, ajungem să recunoaștem cele ce urmează. Putem încerca să luăm în serios împărțirea ființei omenești, despre care am discutat adesea chiar și în aceste conferințe, așa cum trebuie să fie ea. Putem vorbi de faptul că organizarea cap a omului, cu centrarea ei în sistemul nervos-senzorial, are în sine o anumită autonomie; la fel sistemul ritmic, cu tot ceea ce ține de acesta; în sfârșit sistemul metabolic, cu tot ceea ce mai intră în organizarea membre, este și el într-un fel autonom în sine. În organizarea omenească putem deosebi așadar trei sisteme independente și, dacă aplicăm aici în mod rațional principiul metamorfozei, care de altfel trebuie aplicat neapărat la natura organică, vom putea, prin prisma principiului metamorfozei, să ne formăm reprezentări despre raportul reciproc dintre aceste trei componente ale organizării omenești.
Vă rog să mă înțelegeți corect! Vrem să ne facem o reprezentare, chiar dacă pentru început nu va fi decât una schematică, a modului în care se corelează aceste trei componente ale organizării omenești între ele. La prima vedere acest lucru va fi greu de realizat. Va fi greu ca în organele pe care le găsim în cap să recunoaștem clar organele care stau la baza sistemului metabolic membre. Dacă însă se pătrunde atât de departe în morfologia omului, așa cum am indicat eu, dacă aprofundăm într-adevăr reprezentarea, vom reuși să sesizăm într-un anume fel că în raportul reciproc dintre osul lung și osul cranian avem de-a face cu o întoarcere completă a suprafeței interioare a osului în afară – așa cum se întoarce pe dos o mănușă –, la care întoarcere pe dos se întâmplă în același timp o modificare a raporturilor de forțe. Dacă aș întoarce interiorul osului lung în afară la fel cum aș întoarce o mănușă, ar lua naștere tot un os lung, desigur. Dacă însă avem în vedere că osul lung s-a configurat doar după cum am arătat eu, prin orientare radială spre interior pe toată lungimea, fiind obligat deci ca dispunerea de material să o facă pe direcție radială, și apoi îl întorc pe dos, astfel ca interiorul să vină în afară și dispunerea pe care o va face să urmeze apoi nu orientarea radială ci sferoidală, atunci interiorul, care acum se orientează spre sferoidal, capătă exact forma din figura 1.
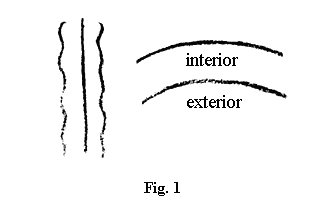
Exteriorul de dinainte este acum interior și viceversa. Dacă dumneavoastră veți urmări îndeaproape acest proces pentru cazul extrem, cel al transformării osului lung în os cranian, atunci vă veți spune: Terminațiile extreme ale organizării omenești, sistemul locomotor și sistemul cranian, reprezintă oarecum poli ai organizării; dar noi nu trebuie să gândim acești poli în mod simplu, opuși liniar, ci presupunând, atunci când trecem de la un pol la celălalt, și existența unei zone de tranziție între rază și suprafața sferică. Fără ajutorul reprezentărilor acestea, așa de complicate, ar fi absolut imposibil să căpătăm o reprezentare adecvată despre organismul omenesc.
Deci acel ceva care formează oarecum mijlocul, veriga mediană a organizării omului, deci acel lucru care este subordonat organismului ritmic, se va afla în mijloc, va forma oarecum un fel de tranziție de la structura radială la structura sferoidală. Morfologic, întreaga organizare omenească trebuie înțeleasă acum prin prisma acestui principiu. Deci trebuie să ne fie clar că dacă luăm un organ oarecare din organizarea metabolică, cum ar fi, de exemplu, ficatul sau unul din organele care aparțin în modul cel mai exemplar metabolismului – nu putem spune decât „aparțin în modul cel mai exemplar”, căci altfel lucrurile sunt întotdeauna amestecate –, deci dacă luăm un astfel de organ și apoi căutăm în organizarea cap organul metamorfozat prin întoarcere pe dos care să-i corespundă, vom constata, desigur, dacă vrem să deslușim forma, o deformare enormă [Nota 170] a respectivului organ. De aceea va fi dificil să surprindem chestiunea matematic. Fără însă să încercăm o abordare matematică nu vom reuși să ajungem la nici un rezultat. Și dacă reflectați – luați-o doar ca o imagine – la faptul că în înțelegerea formei umane există ceva ce ne trimite afară, la mișcările corpurilor cerești, va trebui, dacă vrem să sintetizăm ceea ce apare în mișcările corpurilor cerești, să surprindem aceasta într-un mod asemănător; să nu mai procedăm ca și cum lucrurile se petrec într-un mod de care ne putem apropia doar cu acea geometrie care operează cu spațiul obișnuit și, pentru că face acest lucru, nu poate calcula și cu operația de întoarcere pe dos. Atunci când este vorba de această întoarcere pe dos, așa cum am prezentat-o eu, nu mai putem opera cu spațiul obișnuit. Spațiul obișnuit intervine acolo unde se construiesc în sensul obișnuit cubaje. Dacă însă sunt nevoit să fac din interior exterior, posibilitatea de a continua să calculez cu ajutorul reprezentărilor pe care le am în spațiul obișnuit încetează.
Dacă însă forma omenească trebuie să mi-o reprezint folosind în mod corespunzător întoarcerea pe dos, va trebui ca și mișcările corpurilor cerești să mi le reprezint în așa fel, încât să folosesc pentru ele întoarceri pe dos. Deci sub nici o formă nu pot proceda în același fel în care procedează astronomia, care pentru înțelegerea fenomenelor cerești se slujește doar de spațiul obișnuit, rigid. Dacă luați pentru început doar organizarea cap și organizarea metabolică a omului, va trebui, dacă vreți să treceți de la una la cealaltă, să vă imaginați o astfel de întoarcere pe dos și, în plus, să presupuneți și variații ale formelor. Să căutăm, pentru început, să ne reprezentăm plastic așa ceva.
Am pregătit deja terenul pentru asta, atunci când am indicat curba lui Cassini [Nota 171] precum și acel mod de a concepe cercul nu ca pe o curbă simplă, în care fiecare punct al ei este egal depărtat de un punct central, ci ca pe o curbă în care fiecare punct al ei se află la o astfel de distanță de două puncte fixe, încât câtul celor două distanțe este o mărime constantă. Aici cercul este dat prin intermediul unui alt mod de a vedea lucrurile. Noi am indicat mai întâi curba lui Cassini și am arătat că aceasta are în principal trei forme: una din ele este eliptică, așa cum v-am spus. Ea ia naștere atunci când între constante există un anumit raport, pe care l-am indicat; a doua formă este lemniscata; a treia se prezintă în așa fel încât, din punct de vedere al reprezentării, există o unitate, la fel și din punct de vedere analitic, dar concret ea nu apare ca o unitate. Aceste două ramuri ale curbei lui Cassini sunt de fapt o singură curbă. Când trasăm însă a doua ramură trebuie să părăsim spațiul și să revenim din nou în spațiu atunci când trasăm prima ramură. Din punct de vedere teoretic noi facem o singură mișcare a mâinii atunci când desenăm pe hârtie aceste două domenii, practic separate unul de altul. În spațiul obișnuit nu putem duce aceste linii, dar din punct de vedere noțional ceea ce avem sus și ceea ce avem jos nu constituie altceva decât o singură linie (fig. 2). V-am mai spus însă că această curbă se poate imagina și într-un alt mod. Ea se poate imagina punându-ne următoarea întrebare: Care este traiectoria pe care trebuie să o parcurgă un punct, luminat dintr-un punct fix A, astfel ca intensitatea luminoasă cu care este vizualizat dintr-un alt punct fix B să fie aceeași? Deci aici obțin curba lui Cassini ca pe un loc geometric al punctelor care, luminate dintr-un punct fix A, pot fi observate în alt punct fix B mereu cu aceeași intensitate luminoasă.
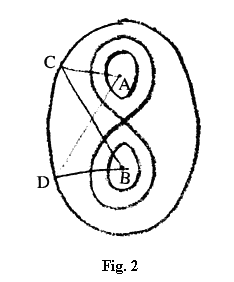
Acum nu va fi greu să vă reprezentați că, dacă ceva luminează din A în C și apoi prin reflexie luminează în B, atunci acesta trimite aceeași strălucire dacă luminează din A în D și așa mai departe. Acest lucru vi-l puteți reprezenta fără prea mare greutate. Ceva mai greu va fi însă să vă formați o reprezentare atunci când ajungeți la lemniscată. Aici deja nu mai este chiar așa ușor să faceți măsurători cu compasul conform legilor reflexiei și așa mai departe. Și cu adevărat greu va fi să vă reprezentați că din punctul B din ramura curbei lui Cassini care înconjoară pe B se observă mereu aceeași intensitate luminoasă venind dinspre A. Greutatea se datorează faptului că la trecerea dintr-o ramură în cealaltă raza de lumină iese din spațiu, după care revine din nou în spațiu luminând. Ar fi aceeași dificultate care există atunci când cineva ne-ar cere să trasăm cu mâna în spațiu cele două ramuri dintr-o singură mișcare. Fără ajutorul acestei reprezentări nu vom reuși să găsim metamorfoza sau apropierea dintre formele unui organ oarecare din cap și un organ oarecare al sistemului metabolic al omului. Dacă vreți să găsiți acea legătură, atunci va trebui neapărat să ieșiți din spațiu. Oricât de ciudat, oricât de paradoxal ar suna asta, ea se traduce în felul următor: Dacă vreți să treceți de la înțelegerea unei anumite forme a capului dumneavoastră la înțelegerea unei anumite forme din cadrul sistemului dumneavoastră metabolic, atunci nu mai puteți rămâne în spațiu, trebuie să ieșiți din dumneavoastră înșivă și să căutați ceva ce nu se află în spațiu, care este tot atât de puțin localizat în spațiul obișnuit cât este ceea ce se află între ramura superioară și cea inferioară a curbei lui Cassini. Aceasta nu este decât un alt fel de a spune că trebuie să ne reprezentăm metamorfoza ca o întoarcere completă pe dos.
Acum, dacă aici noi încă ne mai reprezentăm legătura dintre ramura superioară a curbei discontinue a lui Cassini și ramura inferioară, atunci folosim constante adevărate, invariabile, constante fixe. Dacă însă facem constantele să fie ele însele variabile, așa cum am făcut, există chiar posibilitatea, în cazul constantei variabile, deci în cazul ecuațiilor cu variabilă dublă [Nota 172], să ne reprezentăm ramura superioară și ramura inferioară ca în figura 3. Vom descoperi, fără îndoială, că ramura superioară ia această formă. Dacă deci modificați curba lui Cassini, luând în locul constantelor adevărate tot niște variabile, adică în locul constantelor invariabile puneți funcții [Nota 173], atunci veți obține două ramuri diferite. Dedesubt am putea avea o situație în care una din ramuri vine oarecum din infinit și se duce iarăși mai departe în infinit. Acest raport este însă punctul de plecare atunci când urmăriți anumite forme din cadrul capului omenesc, pe care le exprimați sub formă de curbe și apoi le comparați cu formele anumitor legături organice din cadrul sistemului metabolic, pe care de asemenea le exprimați sub formă de curbe. Aici este cuprinsă întreaga complicație a formei umane. Chestiunea desigur nu devine mai simplă atunci când trebuie să vă reprezentați și că una din linii are o tendință de orientare spre exterior, iar cealaltă linie o tendință de orientare spre interior (fig. 4).
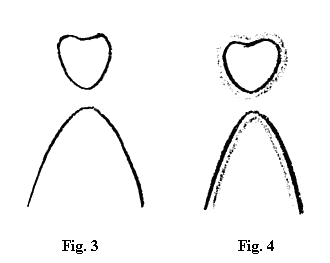
Veți spune – sper să nu-i dați o importanță prea mare, ci să o simțiți doar ca o dispoziție trecătoare: înseamnă că această organizare omenească este într-atât de complicată, încât aproape putem renunța să o înțelegem. În aceasta se exprimă comoditatea mentalității filistine obișnuite, care se practică astăzi în fiziologie și anatomie. Aici nu este nevoie să te obosești atât de tare, nu trebuie să lași reprezentările să dispară, și de fapt să nu dispară, să întorci pe dos imaginile și lucruri de genul acesta! – Dar nici nu vom ajunge să înțelegem organizarea omenească, ci doar ne vom lăsa pradă iluziei că am fi ajuns să o înțelegem.
Deci, dacă pătrundeți astfel cu privirea în organizarea omenească și veți spune: În organizarea omenească există ceva ce se sustrage spațiului, ceva ce nu se găsește înăuntru, în spațiu, ceva ce mă obligă să-mi imaginez că am niște sisteme de curbe separate între ele în spatiu, legătura dintre acestea urmând un alt principiu decât cel oferit de către spațiul nostru tridimensional – atunci probabil nu veți fi nici foarte departe de a vă reprezenta, pentru început doar formal, ceea ce decurge de aici. Nimeni nu poate obiecta pentru început ceva împotriva reprezentării formale a ceea ce voi spune acum, fiindcă aici este vorba doar să ajung la o reprezentare, în același mod ca în matematică. Aici nimeni nu poate obiecta că problema nu s-ar putea demonstra, sau ceva de genul acesta. Și asta pentru că aici este vorba doar de a ajunge la o reprezentare unitară în sine.
Imaginați-vă că nu ați avea de-a face cu spațiul obișnuit, care are deci trei dimensiuni oarecare, ci că ați avea de-a face cu un antispațiu [Nota 174]. Pentru început îl voi numi antispațiu și, ca o primă modalitate de reprezentare, l-aș face să ia naștere în felul următor: imaginați-vă că în reprezentare aș construi spațiul obișnuit, tridimensional, fix; construiesc prima dimensiune, construiesc a doua dimensiune și construiesc a treia dimensiune (fig. 5). Prin faptul că am construit aceste trei dimensiuni am realizat oarecum, cu ajutorul reprezentării, umplerea a ceea ce mi se oferă drept spațiu tridimensional obișnuit. Dumneavoastră știți însă că în orice lucru putem nu numai să înaintăm până la o anumită intensitate, ci și să regresăm, să luăm din ce în ce mai mult din ea și să ajungem apoi la negativ. Știți că nu avem numai posesiuni, ci și datorii. Pot să fac nu numai să apară cele trei dimensiuni, ci și să dispară. Să-mi reprezint procesul de apariție și dispariție ca un proces real, ca ceva ce există. Pot să am reprezentări chiar și în două dimensiuni, dar nu asta am în vedere acum, ci următorul lucru: faptul că aici am doar două dimensiuni nu înseamnă că niciodată nu am avut o a treia dimensiune, ci doar că ea mi-a dispărut din nou. Cele două dimensiuni sunt rezultatul mai întâi al apariției și apoi a dispariției celei de a treia dimensiuni. Așadar acum am un spațiu care exterior mai prezintă doar două dimensiuni, interior însă trebuie să mi-l reprezint având de două ori dimensiunea a treia, una pozitivă și una negativă; dimensiunea negativă provine din ceva care nu poate să se mai afle în interiorul spațiului meu tridimensional, și desigur nu trebuie să mi-o reprezint în sensul obișnuit, ca pe o a patra dimensiune, ci ca pe ceva care se raportează la dimensiunea a treia precum negativul la pozitiv (fig. 6).
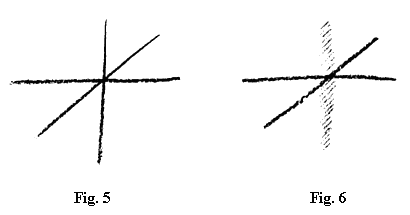
Presupuneți acum că la ceea ce ne-am construit noi aici aș mai insera ceva (fig. 7); aceasta ar putea exista cumva real, însă în felul în care sunt reale de cele mai multe ori în viață lucrurile, realitatea reproducând doar aproximativ, nu chiar scrupulos la fel, ceea ce am prezentat aici. Asta nu trebuie să ne mire în mod deosebit, dat fiind faptul că și în realitatea senzorială exterioară figurile matematice le găsim exprimate tot aproximativ. Nici în acest caz nu trebuie să pretindeți ca lucrurile să stea altfel decât aproximativ la fel, atunci când caut o realitate pentru această imagine. Imaginați-vă totuși că ar trebui să schițez o realitate care să corespundă cât de cât acesteia; atunci nu ar trebui să o desenez riguros la fel, ci să fac ceva aplatizat, ceva care îi corespunde.
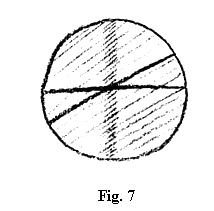
Acum, faptul că aici a fost ceva și apoi iarăși a dispărut, aș vrea să-l reprezint, să zicem, prin nașterea unei densități a acțiunii, indicată prin hașurarea mai pronunțată, dar care a scăzut din nou în intensitate (fig. 8). Aici aveți o sferă care are propriu-zis în mijloc o parte densificată. Vă rog acum, conform acestui principiu, să comparați ceea ce am prezentat în figura 8 în primul rând cu sistemul cosmic real, așa cum se arată el privirii noastre: sfera cu stelele mai rarefiate și sistemul stelar mai aglomerat pe care în mod obișnuit îl numim sistemul Căii Lactee. Comparați însă și hărțile cerești obișnuite. Veți găsi că această imagine – vă rog să ne rezumăm pentru început la a privi aceasta ca o imagine – nu diferă de ceea ce se prezintă de obicei drept trecere a Soarelui sau a Pământului de-a lungul cercului zodiacal, în timp ce acolo undeva, afară (sus și jos), s-au strămutat polii Nord și Sud. După cum vedeți, în ceea ce privește reprezentarea care s-a construit aici nu sunt chiar așa de departe de ceea ce există în realitatea exterioară. Raporturile reale le vom cerceta în conferințele care urmează.
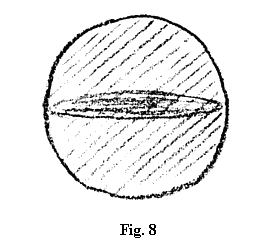
Pentru a putea înțelege însă ceea ce s-a enunțat mai înainte în legătură cu omul, nu este suficient ce am dezvoltat noi aici, ci va trebui să mergem mai departe. Va trebui să spunem: Vom face să dispară și cea de-a doua dimensiune, astfel încât să obținem doar o dimensiune, o dreaptă; această dreaptă însă nu este chiar o dreaptă trasată simplu în spațiul tridimensional, ci ea a rămas încă acolo după ce am făcut să dispară dimensiunile a treia și a doua. Și acum facem să dispară și cea de a treia dimensiune, astfel încât obținem pur și simplu punctul. Să reținem că punctul l-am obținut prin dispariția celor trei dimensiuni și să presupunem că acest punct ni se înfățișează în realitatea exterioară ca ceva de sine stătător. Dar cum trebuie să ne reprezentăm acțiunea sa în cazul în care el apare ca ceva activ? Dacă ne reprezentăm acțiunea sa, atunci această acțiune nu o putem pune în legătură cu un punct oarecare, aflat, să zicem, pe axa x din spațiu, căci aceasta nu există, a dispărut. Nu am putea să o raportăm nici la ceva care are o coordonată x și o coordonată y, căci nici acestea nu există, ele au dispărut din spațiu. De asemenea, nu am putea să-l raportăm, în ceea ce privește acțiunea sa, nici la o a treia dimensiune a spațiului, ci ar trebui să spunem: Dacă el își face simțită acțiunea, atunci va trebui să-l raportăm la ceea ce se află complet în afara spațiului tridimensional. Conform procedeului de gândire folosit, este imposibil să-l raportăm la ceva aflat în interiorul spațiului tridimensional. Putem să îl raportăm doar la ceva aflat în afara spațiului tridimensional, nu la un „x anulat”, un „y anulat”, un „z anulat”, ci la ceva ce anulează x, y, z, care deci nu există în spațiul tridimensional.
Noi am construit asta mai întâi ca o reprezentare formală. Această reprezentare însă devine în cel mai înalt grad reală. Devine foarte, foarte reală dacă nu procedăm conform reprezentărilor științifice comode, cu care se încearcă să se stăpânească lucrurile astăzi, ci ne cufundăm mai profund în lucruri. Analizați, de exemplu, legătura procesului vizual cu organizarea ochiului, încercând efectiv să înțelegeți ceva. Priviți cum se prezintă toată această organizare a ochiului. Știți probabil, am menționat-o deseori în alte conferințe [Nota 175], că ochiul trebuie înțeles nu ca un proces de organizare obișnuită, din interior spre exterior, ci ca ceva format din exterior spre interior. Organizarea din afară spre interior o putem înțelege urmărind filogenetic formarea animalelor inferioare și apoi trecând la procesul vizual. Dacă studiați procesul vizual, trebuie să încercați să vă transpuneți interior în felul cum este el stimulat din afară, cum se adaptează acest organ pentru a putea fi de asemenea stimulat din afară, cum mai departe acțiunea se continuă în interior spre nervul optic și trece apoi în organizarea generală, dispărând oarecum în organizarea generală. Putem găsi desigur terminația nervilor optici însă, dacă intrăm în organizarea mai fină – este ceva exprimat aproximativ –, putem deja spune: El se pierde în această organizare. Dacă comparați cât se poate de conștiincios acest proces vizual, și organele ce țin de el, cu procesul de secreție al rinichilor de exemplu, atunci calea de evacuare în cazul secreției rinichilor trebuie pusă în legătură cu ceva ce dincolo se pierde treptat din exterior spre interior, prin trecerea organului vizual în nerv optic.
Dacă vreți să obțineți reprezentările care pun în legătură aceste două lucruri și astfel să puteți înțelege fenomenele care au loc în cazul unui proces sau altul, atunci trebuie să vă slujiți
de reprezentări de genul celor indicate anterior. În momentul în care pentru procesul vizual vă formați reprezentări în spațiul tridimensional și apoi căutați corespondentul în cazul procesului
de secreție al rinichilor – putem pune, desigur, un proces în locul celuilalt – trebuie să vă imaginați acțiunea ca și când ieșiți din spațiul tridimensional. Trebuie să parcurgeți un proces de
gândire exact la fel cum am procedat atunci când am realizat anularea dimensiunilor; altfel nu vă veți descurca.
În mod asemănător trebuie să procedați dacă vreți să înțelegeți curbele ce rezultă atunci când cercetați traiectoriile lui Venus și Mercur, inclusiv buclele ce se pot observa obișnuit pe cer cu
ochiul liber, și apoi traiectoriile lui Jupiter și Marte. Dacă folosiți, să zicem, sistemul de coordonate polare, puteți lua pentru bucla lui Venus originea acestui sistem în cadrul spațiului
tridimensional. Aici puteți face acest lucru. Nu veți ajunge însă la nici un rezultat dacă vreți să înțelegeți, de pildă, bucla lui Marte conform aceluiași principiu. Aici trebuie să presupuneți
în mod ideal că originea sistemului de coordonate polare se află în afara spațiului tridimensional. Și mereu veți fi obligați să luați coordonatele în așa fel, încât o dată – să zicem pentru
orbita lui Venus și a buclei sale – porniți de la un pol al sistemului de coordonate și presupuneți aceste coordonate pornind dintr-un punct (fig. 9); altă dată, pentru orbitele lui Jupiter sau
Marte și a buclelor lor, ca să ajungeți la un rezultat trebuie să spuneți: Nu voi lua o astfel de origine a sistemului meu de coordonate polare, unde, pentru a obține coordonatele, trebuie mereu
să adaug ceva, ci voi lua ca origine a sistemului meu de coordonate polare sfera, deci tot ceea ce se află dincolo, în nedefinit (fig. 10), și voi avea atunci drept coordonate liniile
întrerupte; pentru acestea trebuie mereu să scad, să dau la o parte ceva. Voi obține în acest caz o linie, care și ea are un fel de centru, dar acest centru se află în sfere infinite.

Ar putea fi necesar deci, pentru a putea urmări mai departe orbitele planetelor, ca la constituirea orbitelor planetelor interioare să ne reprezentăm că ele au un centru al lor aici, în spațiul obișnuit, dar atunci când vrem să ne reprezentăm niște centre pentru orbitele lui Jupiter, Marte și așa mai departe să fim nevoiți să ieșim din spațiul obișnuit.
Aici trebuie să transcendem spațiul. Este absolut necesar acest lucru. Dacă încercați să înțelegeți fenomenele într-un mod cu adevărat riguros, veți vedea că folosind reprezentările obișnuite din spațiul tridimensional nu veți reuși să vă descurcați. Va trebui să luați în considerare conlucrarea dintre un spațiu care are cele trei dimensiuni obișnuite, pe care în mod ideal vi-l puteți imagina extinzându-se radial dintr-un centru, și un alt spațiu care distruge permanent acest spațiu tridimensional, pe care acum nu mai avem nevoie să ni-l imaginăm pornind dintr-un punct, ci trebuie să ni-l imaginăm pornind dintr-o sferă infinit depărtată; deci o dată punctul având o arie egală cu zero, iar altă dată o arie egală cu cea a suprafeței unei sfere infinit de mari. Trebuie să distingem deci două feluri de puncte: un punct având suprafața egală cu zero, orientată spre exterior, și un punct având o arie egală cu suprafața unei sfere infinit de mari, orientată spre interior. În domeniul pur geometric este suficient dacă ne reprezentăm un punct în mod abstract. În domeniul realității acest lucru nu este suficient. Nu ne putem descurca dacă ne reprezentăm doar punctul abstract. Trebuie să ne întrebăm mereu dacă punctul pe care ni-l reprezentăm este curbat în afară sau în interior, fiindcă în acea direcție se orientează și câmpul său de acțiune.
În plus, trebuie să mai țineți seamă de ceva. Puteți să vă reprezentați că undeva aveți un punct, care este o sferă (fig. 11, cercul continuu). Pentru început nu este necesar să vă reprezentați punctul infinit depărtat chiar în (a). Putem să ni-l imaginăm și puțin mai departe (b, c). Toate punctele vi le puteți reprezenta oriunde în afară, însă doar această sferă (cercul interior) trebuie să o lăsați liberă, căci ea este golită întru câtva. Ea este cercul inversat, sau sfera inversată, dacă vreți.
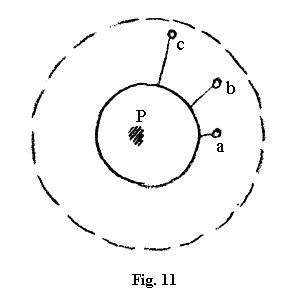
Gândiți-vă însă că avem următoarea situație: ceea ce există în afara cercului abstract [Nota 176] (cercul continuu), deci acest punct având curbura orientată spre interior – căci tot acest spațiu din afara suprafeței sferice (cercul continuu) nu este altceva decât un punct, având curbura orientată spre interior – ar fi și el delimitat undeva. Deci puteți merge departe, dar realitatea este că nu puteți ajunge chiar peste tot, căci undeva avem din nou o graniță, de o cu totul altă factură (cercul întrerupt). Care ar fi consecința acestui fapt? Consecința ar fi că undeva (P) ar trebui să apară ceva care să aparțină din nou realității existente acolo, afară. Aici în interior ar trebui să apară o sferă mică [Nota 177], care ține de ceea ce există acolo, afară. Ar trebui deci să spuneți: Acolo, în afara unei sfere există ceva; acest ceva existent afară eu nu-l pot vedea însă decât privind aici (P), înăuntru. Căci ceea ce apare din nou aici, ceea ce se ivește aici este continuarea a ceea ce există acolo, afară. Ceea ce caut atunci când merg în depărtările infinite îmi apare din nou venind dinspre centru.
Se pot dezvolta oricât de multe astfel de reprezentări. Ele oricum fac impresia a ceva ce, formal chiar, este perfect îndreptățit. Dar dacă și încercăm să pătrundem cu astfel de reprezentări ceea ce este real din punct de vedere exterior, facem un lucru cu totul deosebit. Gândiți-vă că în interiorul spațiului ceresc ar exista un fenomen, să îl numim pentru început Lună. Acest fenomen nu ar putea fi înțeles spunând simplu: Luna este un corp, își are centrul aici și noi o cercetăm conform principiului că ea își are centrul aici și este un corp. – Presupuneți – iertați-mă dacă vorbesc puțin eufemistic – că acest fel de a gândi nu se potrivește realității, ci că ar trebui să vorbesc altfel, că ar trebui să spun: Dacă în lumea mea pornesc dintr-un punct și merg mereu mai departe și mai departe, voi ajunge până acolo unde nu mai întâlnesc alte corpuri cerești, unde, dacă este să vorbim totuși de o realitate, nu mai putem întâlni nici măcar spațiul euclidian gol, unde însă găsesc ceva care prin realitatea sa mă determină să gândesc continuarea sa în P. Voi fi nevoit atunci să gândesc conținutul spațial al acestei Luni ca o bucată din ansamblul lumii, cu excepția a tot ceea ce se găsește, stele și așa mai departe, în exteriorul Lunii. Pe de o parte trebuie deci să-mi imaginez tot ceea ce am ca stele în spațiul cosmic (a, b, c din fig. 11). Pe acestea ar trebui să le tratez într-un mod unitar; este o primă ipoteză pe care o fac. Interiorul Lunii însă, volumul ei, nu ar trebui să-l tratez așa, ci doar cum am spus: Pot merge pe de o parte în depărtare. Aici presupun că undeva există sfera – este vorba în primă instanță de sfera aparentă, dar cumva trebuie gândit că la baza ei există și ceva efectiv. Dar tot ceea ce se află în interiorul suprafeței sferice a Lunii nu are nici o legătură cu ceea ce mi se arată acolo, în depărtări; aceasta are o legătură cu ceea ce începe acolo de unde stelele încetează să mai existe. Acest interior este o bucățică ce, în mod curios, aparține nu de lumea mea, ci de lumea căreia nu-i aparține nici o stea. Dacă întâlnim așa ceva într-o anumită lume, avem de-a face cu o intervenție de o cu totul altă natură în lume, având cu totul alte calități interioare decât ceea ce există în jurul ei. Și atunci raportul unei astfel de Luni față de cerul din jurul ei îl putem compara, de exemplu, cu raportul existent între secrețiile rinichilor, cu organismul aferent, și organismul ocular. Mâine vom porni discuția noastră din acest punct.
Nu eu sunt vinovat că trebuie să încerc să vă conturez niște reprezentări complicate despre construcția universului, ci faptul că altfel, cu alte reprezentări, nu te descurci. Te descurci doar dacă spui: Noi cuprindem fenomenele cu aceste reprezentări, după care brusc se ivește o graniță, nu mai poți înainta. Dacă totuși se dau reprezentări atât de complicate pentru a vă introduce în întelegerea universului, de vină nu este o manie oarecare de a dezvolta reprezentări deosebite, ci realitatea însăși.