Rudolf Steiner
ASTRONOMIA ȘI ȘTIINȚELE NATURII

GA 323

NOTE

Observație preliminară: Titlul cursului Astronomia și științele naturii provine de la Rudolf Steiner. El este în concordanță cu fraza din Conferința a XVII-a: „Ceea ce am vrut însă, a fost să vă prezint raporturile astronomiei cu celelalte domenii ale științei”. Cele două subtitluri aparțin editorilor: „Cursul al treilea de științe naturale”, acesta vrea să exprime faptul că el a avut loc în același cadru și cam cu același auditoriu ca la cele două cursuri de științe naturale pure, și anume cercul corpului didactic al școlii libere Waldorf din Stuttgart, întemeiată aproximativ cu 16 luni înainte, și câteva alte personalități, cei mai mulți dintre acestia de formatie naturalist-științifică sau matematică. Rudolf Steiner era conducătorul școlii, iar în cadrul cursului intervin cât se poate de natural chestiuni importante legate de probleme pedagogice. Cu toate acestea el nu este un curs pedagogic, însă elementul antropologic este atât de semnificativ încât deseori poate fi resimțit ca o continuare la Antropologia generală ca bază a pedagogiei (GA 293), curs ținut la înființarea școlii. Astfel a fost necesar un alt titlu care să exprime acest aspect antropologic. Cursul a luat naștere din colaborarea strânsă a lui Rudolf Steiner cu colegiul profesoral al școlii Waldorf. Cititorul de azi trebuie să ia în considerare acest lucru. Ceea ce avem în față nu este un manual, ci mărturia unui eveniment educațional în cadrul unui cerc de personalități (strict delimitat), cărora le-au fost transmise impulsuri puternice de viitor pentru dezvoltarea științelor. Așa cum se poate sesiza, cursul a pretins mult de la auditoriul său și s-a mers până la limita la care ar mai fi existat perspectiva unei înțelegeri. Aceasta însă nu s-a realizat nici până astăzi, decât într-o mică măsură. Întrebări majore, cum ar fi cea referitoare la mișcarea de lemniscată a Soarelui și a Pământului, sunt nerezolvate, cu toate că nu au lipsit strădaniile în acest sens. Cu toate acestea alte probleme ridicate în acest curs s-au arătat fertile în numeroase lucrări, cel mai mult probabil problema „antispațiului” (Conferința a XV-a), asupra căreia una dintre note ne va orienta mai în amănunt. – Cursul nu este deci un manual de astronomie sau de științe naturale. De fapt, el presupunea cunoștințe de nivel școlar despre lucrurile tratate. Doar în felul acesta au ajuns cei ce audiau cursul să perceapă libertatea dinăuntrul căreia se utilizau aceste cunoștințe. Aici s-au pus și problemele editoriale. Un exemplu le poate ilustra: pentru descrierea buclelor planetare (Conferința a XI-a) se atribuie planetei Mercur – printr-o simplificare îndrăzneață – o singură buclă într-un an, la fel ca la toate celelalte planete. Această afirmație nu este conformă cu manualul de astronomie, căci Mercur face trei bucle într-un an. Pasajul a și apărut corectat în prima ediție. În ediția actuală s-a revenit la textul originar. În anii '60 s-a arătat de fapt că în ceea ce privește cunoștințele despre planeta Mercur nu era încă totul pus la punct. Până atunci, deci până în epoca zborului spre Lună, durata rotației sale era indicată peste tot greșit! Acum ne întrebăm cum de s-a putut întâmpla așa ceva. Răspunsul este: fiindcă numai fiecare a treia buclă făcută de Mercur se poate observa bine, iar durata de rotație se calculase efectiv doar din observațiile făcute la fiecare a treia conjuncție. Prin aceasta însă avem acea unică buclă într-un an! Acest pasaj din curs nu-l putem înțelege astăzi altfel decât ca o provocare, în sensul de a ne ocupa mai exact cu problema lui Mercur. Din acest exemplu mai reiese și că editarea nu putea fi făcută fără niște indicații amănunțite. Aceasta s-a văzut de fapt încă de la prima apariție, când nu s-au putut evita câteva note de subsol. – Caracterul cursului, așa cum este exprimat direct în Conferințele a IV-a și a VII-a și după cum reiese indirect din alte pasaje, nu este cel al concepției spirituale, ci unul care se adresează intelectului, spre deosebire de marea majoritate a expunerilor antroposofice ținute de Rudolf Steiner. Este vorba de intelectul uman sănătos, capabil, așa cum explica adesea Rudolf Steiner, să aprecieze rezultatele contemplării spirituale.

Cu acest curs s-a întâmplat ceva special și anume: încă înainte să existe ediția din 1926, el a fost prelucrat după notițe de către dr. W. Kaiser, pe atunci aspirant II în filosofie, și a devenit o lucrare care s-a publicat. Cartea a apărut în 1925 în Stuttgart sub titlul Astronomia în lumina științei spiritului. Puțin înaintea morții sale, Rudolf Steiner a apucat să vadă manuscrisul și a încuviințat tipărirea. Lucrarea nu conține numai un referat al cursului, ci și confruntarea autorului cu multe probleme care se ridică pe parcursul lui. Aceasta a rămas singura scriere care tratează cursul în întregul lui. Un an mai târziu, ea a ieșit de sub tipar sub îngrijirea dr. Elisabeth Vreede, șefa secției de matematică-astronomie de la Goetheanum. Editorii ediției prezente au avut prin aceasta un mare ajutor pentru a putea clădi în continuare, pe baza muncii ce s-a depus la prima ediție. În notele care urmează, acolo unde nu este menționat altceva, compararea de text se referă la această primă ediție.

Documentele care au stat la baza textului: stenograma de bază și copiile dactilografiate după aceasta provin de la Hedda Hummel. Stenograma s-a pierdut, în timp ce copii ale acesteia mai există încă. Se pare că la baza textului primei ediții a stat doar o astfel de copie. Spre deosebire de aceasta, ediția prezentă a avut posibilitatea de a folosi notițele stenografiate private făcute în timpul cursului de doi auditori, unele foarte amănunțite, ale dr. Karl Schubert, și unele mult mai sumare, ale dr. med. Eugen Kolisko. Ambii au participat la curs în calitate de profesori de școală Waldorf. Notițele concordă în unele locuri cuvânt cu cuvânt, pentru ca apoi să fie rezumate. Lipsesc pasaje întregi. Cu toate acestea ele s-au dovedit de un real folos pentru lămurirea acelor pasaje care ridicau semne de întrebare. Descifrarea notițelor stenografiate ale lui Gabelsberger se datorează domnului Richard Schönberg și domnului Günther Frenz. În total există cam 70 de modificări în text datorate acestei stenograme. Atunci când ne referim la ele în trimiterile care urmează, sursa lor va fi indicată prin cuvântul „stenogramă”. Notițele de care vorbeam mai conțin multe desene, care au contribuit la stabilirea figurilor schițate în timpul prelegerii. – Acolo unde textul de față se abate de la textul primei ediții este vorba fie de corecturi pur stilistice, fie de corecturi propriu-zise. Primele sunt mai numeroase, deoarece cele două texte nu au același obiectiv. Prima ediție era destinată ca material de lucru pentru un cerc de persoane și trebuie privită ca o lărgire a cercului auditoriului inițial. De aceea această lucrare a și fost vândută în exemplare numerotate, nu pentru lectură, ci pentru lucru, în special pentru cercetarea personală în direcțiile amintite. Aceasta a fost intenția inițială a lui Rudolf Steiner în ceea ce privește cursurile de acest fel. Pentru ediția operelor complete nu mai există o astfel de restricție. Această ediție ridică alte exigențe, privitoare la forma textului, exigențe care au condus la modificări stilistice. Corecturile propriu-zise merg de la corecturi obișnuite până la cele de mare răspundere, cum ar fi completarea cuvintelor lipsă sau chiar a unor grupe de cuvinte. În măsura în care aceste corecturi, inevitabile ținând cont de prescurtările specifice stenogramelor și de faptul că se vorbea liber, s-au făcut și la prima ediție, ele s-au preluat aproape fără excepție în textul nou. Puținele locuri unde s-a revenit la copie au fost menționate în cele ce urmează. Nu s-au menționat corecturile stilistice și cele neimportante, ci doar cele care pot avea o legătură cu sensul, înțelegerea și interpretarea expunerilor. Același lucru este valabil și pentru modificările datorate stenogramei. Unele dintre acestea arată încă o dată cât de mult pot fi deformate copiile datorită erorilor de citire a stenogramelor și implicit arată importanța unei stenograme originale. Unde lipsește așa ceva dispare și speranța de a putea corecta atâtea și atâtea cuvinte, care doar „grație stenogramei” au găsit posibilitatea de a fi rectificate. Căci cine ar putea să-și dea seama, de exemplu, fără stenogramă, că „precum se obișnuiește” trebuie citit „precum geologii” (Conferința a II-a)*.

* În germană: wie gewönlich și wie Geologen.

1. Nikolaus Copernicus, Thorn, 1473–1543, Frauenburg. Întemeietorul astronomiei moderne.
   
   Galileo Galilei, Pisa, 1564–1642, Arcetri, lângă Florența. Unul dintre pionierii dezvoltării științelor naturii.
   
   Johannes Kepler, Weil der Stadt (Württemberg), 1571–1630, Regensburg. Continuatorul noii astronomii a lui Copernic. Bazându-se pe observațiile lui Tycho Brahe el descoperă cele trei legi ale mișcării planetelor ce-i poartă numele.
2. În mod corespunzător... omenirea va face alte investigații: În copie este scris „investigații” în loc de „concluzii”, ceea ce are sens dacă fraza se completează așa cum s-a arătat aici.
3. Immanuel Kant, Königsberg, 1724–1804 – în același loc. Textual, cugetarea sa sună astfel: „Eu afirm însă că în fiecare obiect de studiu putem găsi atâta știință propriu-zisă câtă matematică se află în ea” (Prefață la lucrarea Principii metafizice elementare ale științelor naturii, publicată în 1786).
4. Emil Du Bois-Reymond, Berlin, 1818–1896, tot aici. Renumitul său discurs Despre limitele cunoașterii a avut loc cu ocazia ședinței publice la cea de a 45-a întrunire a cercetătorilor științelor naturii și medicilor din 14 august 1872 – Leipzig.
5. Sir Isaac Newton, Woolsthorpe, Lincolnshire, 1642–1727, Kensington, Londra. Matematician, fizician, astronom. A formulat pe scurt principiile mecanicii clasice, iar prin aplicarea lor la fenomenele cerești a devenit întemeietorul mecanicii cerești. Opera sa de căpătâi: Philosophiae naturalis principia mathematica, 1687.m
6. Johann Wolfgang Goethe, Frankfurt a. M, 1749–1832, Weimar. Teoria sa despre vertebrele craniene se găsește în Scrieri de știință naturală, editată de Rudolf Steiner în ediția Kürschner Literatura națională a germanilor, 5 volume, reeditare 1975, Dornach, GA 1 a–e, O.C., în vol. I, p. 316. În nota de la subsolul paginii 322 este comentată descoperirea lui Oken din 1807.
   
   Lorenz Oken, Bohlsbach, lângă Offenburg, 1779–1851, Zürich. Și-a publicat teoria despre vertebrele craniene în lucrarea-program prin care a luat în primire catedra de profesor în Jena.
   
   Carl Gegenbaur, Würzburg, 1826–1903, Heidelberg. Anatomist. Lucrările sale sunt: Despre nervii capului la hexanchus și raportul lor cu teoria vertebrelor craniene, „Revista de științe naturale din Jena”, vol. 6, 1871; Scheletul capului selachienilor, o contribuție la cunoașterea genezei scheletului capului la animalele vertebrate. Cercetare de anatomie comparată la animalele vertebrate, Caietul 3, Leipzig, 1872.
7. Acest alt pol este...embriologia: prin aceasta se reia firul care este legat de finalul la Al doilea curs de științe naturale (conferința a 14-a din Impulsuri spiritual-științifice pentru dezvoltarea fizicii, GA 321).
8. prima treime a secolului al XIX-lea: conform stenogramei, în loc de „mijlocul lui...”.
9. fig. 8: figura este detaliul m din figura 7, mărit, nefiind clar dacă ea așa a fost făcută sau dacă a fost doar indicată în cadrul detaliului m.
10. în sine acel repaus al macrocosmolului: „în sine”, adăugat.
11. chiar în sensul acestei linii de forță: rămâne deschis la ce linii s-a făcut referire în discuție.
12. la domenii care, din punct de vedere al obiectului studiat, sunt apropiate: „al obiectului studiat”, în loc de „al lui”.
13. o maximă, pe care Goethe: s-a avut în vedere desigur fraza „Omul nu înțelege niciodată cât de antropomorf este”. Vezi nota de la p. 28, vol. V, Maxime în proză, p. 353.
14. „ce grozav de departe”: din Faust de Goethe, I, Noapte (cameră gotică), Wagner în convorbire cu Faust.
15. Vechii caldeeni aveau observații: este remarcabilă cunoașterea lor în ceea ce privește perioadele de repetare a evenimentelor. De exemplu, ciclul de 19 ani, botezat după numele grecului Meton, de repetare a pozițiilor Soarelui și Lunii în raport cu stelele fixe. Astrologul grec Rhetorios, pe baza surselor caldeene, enumeră multe perioade de acest fel, de exemplu pentru Marte: 284 de ani = 151 revoluții = 133 perioade sinodice. Ambele cifre, după datele de azi, au o eroare de o zi, deci o eroare relativă de 0,01 miimi (calculat după ani siderali, deoarece conform lui van der Waerden babilonienii nu cunoșteau anul tropic). Rhetorios și alții indică și „ani mari” pentru repetarea identică a unui eveniment, de exemplu în fraza: „Repetarea cosmică are loc în 1 753 005 ani; atunci toți aștrii se adună în Rac la 30 de grade sau în Leu la 1 grad și are loc o revenire completă; însă în Rac este o inundație într-o parte a universului” (conform lui B.L. van der Waerden, Știința care trezește, vol. 2, Basel 1968, pp. 109 și 116).
16. Tycho Brache, Knudstrup, în Schonen, 1546–1601, Praga. A atins o treaptă nouă în ce privește exactitatea observațiilor astronomice. Privitor la „sistemul planetar tychonian”, a se compara pasajul din Conferința a XIII-a și nota corespunzătoare.
17. Pe vremea lui Copernic s-au ciocnit puternic între ele: Rudolf Steiner a vorbit surprinzător de des despre Copernic, mai des de pildă decât despre Kepler, așa cum arată o comparație pe pasaje din lucrările de informare sau vademecum-uri (Adolf Arenson, Călăuză prin 50 de cicluri de conferințe ale lui Rudolf Steiner și Emil Mötteli, Lexicon și registru nominal de sumare, volume rezumative la ediția de opere complete II). Motivul cel mai profund se găsește probabil în conferințele Locașe de Misterii ale Evului Mediu; rosicrucianism și principiul de inițiere modern (GA 233a), conferința a 4-a. A se compara și Conducerea spirituală a omului și omenirii, pp. 81-88 (GA 15, 1974) și Momentul nașterii științelor naturale în istoria universală și dezvoltarea lor de atunci încoace (GA 326). Copernic și-a desăvârșit opera sa despre sistemul planetar heliocentric în anul 1507 însă nu a dat-o publicității. În 1543, când lucrarea De revolutionibus orbium coelestium a fost publicată prin intermediul unui prieten, care a urmărit tiparul și i-a pus o prefață, ce prezenta opera ca pe o metodă de calcul ipotetico-științifică, el se afla deja pe patul de moarte. Copernic a dedicat-o papei Paul al III-lea. În felul acesta ea a trecut de cenzură. Abia după ediția a 3-a, 1616–1671, a fost interzisă. Așa a rămas până în 1822.
18. cât de puțin esențial este ceea ce se ia în considerare: modificat din „se ia în seamă”.
19. a intervenit ceva bizar: „bizar” este adăugat după stenogramă.
20. s-au luat primele două legi de bază ale lui Copernic, a treia s-a lăsat deoparte: În Mécanique céleste, la începutul capitolului „Despre librația Lunii” (vol. V), Laplace face următoarea descriere: „Cei din vechime observaseră că Luna în mișcarea sa în jurul Pământului ne arată mereu aceeași față; dar departe să se mire de așa ceva, ei considerau acest fenomen ca ceva natural pentru orice corp care se rotește în jurul unui centru. Această eroare, sau mai bine zis iluzie, l-a constrâns pe Copernic, pentru a respecta paralelismul axei Pământului, să atribuie acestei axe o mișcare anuală contrară rotației Pământului pe orbita sa, având aceleași neuniformități, ceea ce a complicat considerabil sistemul său. Kepler a fost primul care a făcut observația că paralelismul axei de rotație a unei sfere trebuie să se mențină de la sine în cele mai diverse mișcări ale centrului sferei. Datorită acestei observații, sistemul lui Copernic a devenit mai simplu...”. Rudolf Steiner s-a ridicat mereu împotriva acestei concepții, care există în astronomie, prima oară, probabil în 1906 (în În fața porților teosofiei (GA 95), 1978, p. 105), apoi într-o expunere mai lungă, însă mult mai simplificată din 29.4.1908 (GA 98, O.C., în pregătire). Din nou vine vorba despre aceasta în contextul școlii Waldorf, prima dată, în mod surprinzător, în cursul pregătitor pentru învățători Arta educației. Convorbiri de seminar și conferințe despre programa de învățământ (GA 295, 1977, p. 141). Trei săptămâni mai târziu din nou, în conferințe cu învățătorii. Aceeași temă se tratează într-o conferință pentru membri, ținută tot la Stuttgart (Tratarea spiritual-științifică a problemelor sociale și pedagogice (GA 162, conferința din 28.9.1919). Această abordare repetată în cadrul legăturilor școlare existente în Stuttgart nu se poate înțelege decât prin faptul că ea se adresa personalităților corpului didactic, pe care Rudolf Steiner le vedea în stare să poată face ceva cu aceste expuneri. După anul 1919 tema nu a mai fost abordată, până la cursul de față. Modul în care se vorbește aici în această privință este legat de antecedentele și datele particulare ale acelor personalități cărora li se adresa. Pentru apariția cursului în cadrul Operelor complete trebuie avută în vedere această dificultate. Chiar dacă este imposibil, în puține cuvinte, să creezi un substitut al premiselor existente la auditoriul de atunci, există pe de altă parte o posibilitate vastă de orientare prin intermediul ediției Operelor complete asupra a tot ceea ce vrea să trateze știința spiritului. Din multitudinea de aspecte care ar trebui scoase în evidență, să numim doar câteva: conferințele menționate în trimiterea referitoare la Copernic, p. 39, Locașuri de misterii ale Evului Mediu (GA 233a), dezbat întreaga problemă a concepției copernicane despre lume în profunzimea ei; în ciclul Ierarhii spirituale și reflectarea lor în lumea fizică (GA 110), conferința a 6-a, se compară sistemul cosmic copernican cu cel ptolemeic și pe ambele le caracterizează ca fiind un aspect fizic, respectiv unul spiritual al cosmosului; la sfârșitul conferinței a 3-a din ciclul Excurs în domeniul Evanghelia după Marcu (GA 124), sunt scrise cuvintele: „Din copernicanism, în știința exterioară nu se cunoaște decât partea care ține de ceea ce este pieritor. Partea care trebuie să trăiască în continuare – nu doar cea care a acționat deja în cei 400 de ani, ci cea care trebuie să trăiască în continuare – omenirea trebuie abia să și-o cucerească”; conferința a 12-a din ciclul Evanghelia lui Ioan în raport cu celelalte evanghelii, în special cu Evanghelia lui Luca, (GA112), face o caracterizare foarte temeinică a raportului științei actuale cu vechea clarvedere, care culminează spunând că în știință există cunoaștere adevărată doar în măsura în care noțiunile utilizate de ea provin din vechile concepții metamorfozate, care însă ca noțiuni devin din ce în ce mai diluate. – Pe fondul ultimelor două puncte de vedere pomenite, putem căpăta perspectiva justă relativ la accentul care se pune pe a treia teoremă fundamentală a lui Copemic: este vorba mai mult decât de corectitudine istorică, este vorba de ceea ce are cu adevărat viitor în opera lui Copernic și pe care el a cuprins-o cu un gând genial. – În orice caz, cel care atribuie celei de a treia legi fundamentale o importanță de sine stătătoare nu ia mecanica cerească drept singura competentă. Acesta este cazul, de fapt, aici. O formulare concisă a poziției vizavi de mecanica cerească este conținută într-un pasaj din conferința amintită deja mai înainte, din 28.9.1919: „Și în principal omenirea prezentă se situează încă pe această poziție: de a-și închipui Pâmântul ca pe o sferă mare în spațiul cosmic, iar extrapământescul cuprinzându-l de fapt doar cu reprezentări matematico-mecanice, care cel mult pentru câțiva, care gândesc mai exact, sunt pur matematice, pentru că oamenii mai cuminți au abandonat noțiunile născocite despre tot felul de forțe gravitaționale, și doar imaginea extrapământească a cosmosului este reprezentată matematic. Printre oamenii „mai cuminți” trebuie considerat desigur și Kirchhoff, care va fi amintit în Conferința a VII-a – compară și nota corespunzătoare. Un argument serios împotriva modului de gândire pur mecanic al cosmosului, dezvoltat în multe locuri, este repetat chiar la sfârșitul acestui curs (Conferința XVIII-a). Odată cu abandonarea celei de a treia legi de bază a lui Copernic se face și afirmația că o deplasare a axei Pământului paralel cu ea însăși nu ar modifica locul polului ceresc. De fapt nimeni nu va contesta acum că datorită depărtării finite a stelelor ar trebui să apară o deplasare a polului, în raport însă cu alte neglijări care se produc aceasta este considerată nesemnificativă. Această poziție consideră mărimea unui efect drept criteriu al importanței sale. Fără aceasta, practicianul aproximării matematice ar fi în situația unui luptător căruia i-a fost smulsă arma din mână. Totuși cantitatea, drept criteriu al importanței lucrului, oferă o garanție doar pentru ceea ce a pășit deja în devenire, nu și pentru ceea ce urmează să devină. În marea de mici efecte, imposibil de cuprins cu privirea, este nevoie de un criteriu superior pentru a descoperi efectele semnificative. În sensul cursului de față, trebuie spus că el îți pune în mână tocmai acest criteriu superior, făcând de exemplu puntea între astronomie și structura umană.
21. Elementul matematic... urcă din interiorul nostru: raportul aspectului matematic cu realitatea exterioară este tratat pe larg în prima conferință din volumul Impulsuri spiritual-științifice pentru dezvoltarea fizicii. Primul curs de științe naturale, GA 320, O.C., cu explicații.
22. Vom mai... arăta...: a se compara cu Conferința a XVI-a.
23. durata de timp: în loc de „durată și timp”, conform stenogramei.
24. Dorul de casă îl poate face pe om să zacă în pat bolnav: istoria acestui cuvânt este instructivă. Friedrich Kluge relatează (Programul Universității Albert Ludwig, Freiburg, 1901, p. 26): „Dar ceea ce se ascunde în spatele cuvântului dor de casă nu este de fapt un sentiment clar exprimat referitor la țară. Mărturiile cele mai vechi ale cuvântului pe care le deținem definesc cuvântul ca pe numele unei boli*. Îl întâlnim în primul rând în scrierile de specialitate din medicină.”

    * În germană: Heimweh = dor de casă, Weh însemnând și boală, durere.

25. „magul bătrân și rece cu gușuliță”: expresia nu a putut fi dovedită până acum.
26. precum geologii: în loc de „ca de obicei”* conform stenogramei.

    * În germană: wie Geologen, în loc de wie gewöhnlich.i

27. se poate recunoaște... încă din ziua de azi: Ernst Mach scrie (Dezvoltarea mecanicii, prezentată istorico-critic, 1883, ed. a 7-a, 1912, p. 226): „Dacă rămânem pe tărâmul faptelor, nu cunoaștem decât spații și mișcări relative. Mișcările în sistemul cosmic sunt relative... fie conform concepției ptolemeice, fie a celei copernicane. Ambele concepții sunt de asemenea în mod egal juste, numai că cea din urmă este mai simplă și mai practică”. Filosoful Christian von Ehrenfels vorbește în Cosmogonia sa (Jena, 1916, p. 109) despre preferința pe care o are de fiecare dată pentru ipotezele „cele mai simple”, „cele mai naturale” și „cele mai logice”. Așa s-ar explica și predilecția pentru sistemul solar copernican față de cel ptolemeic.
    
    Ernst Mach, Turas (Moravia), 1838–1916, Haar, lângă München. Fizician și epistemolog.
28. sferei minerale: modificat din „sferei de minerale”.
29. luăm în considerare schimbarea anotimpurilor: corectură la „vremea începuturilor de an”*, în concordanță cu alineatul precedent.

    * În germană: Jahreszeitenwechsel – schimbarea anotimpurilor. Jahreswechselzeiten – vremea începuturilor de an.

30. dinspre latura spiritual-sufletească: „spiritual-sufletească”, în loc de „psihologică”, conform stenogramei.
31. bază solidă pentru niște concepții astronomice adevărate: în loc de „astronomie adevărată”, conform stenogramei.
32. În el mai era încă o conștiență a faptului: „o conștiență” în loc de „ceva”.
33. sau altfel scris: în cele două proporții care urmează termenii sunt altfel dispuși decât la prima ediție, ca urmare a mențiunii dintr-un carnet de notițe (nr. 52, 1921). Prin aceasta, în ultimele proporții avem în dreapta accelerațiile centrale.
34. ... în întregime legea gravitației a lui Newton, dedusă din legea lui Kepler: o deducție asemănătoare se afla în Enciclopedia științelor filosofice a lui Hegel, p. 270.
35. caput mortuum: în traducere mot à mot: „cap de mort”, astăzi folosit în sensul de inutil, neesențial.
36. Va trebui să mai revenim asupra acestui lucru: la aceasta nu s-a mai ajuns.
37. antropomorf: în copie este scris „alchimic”, lucru care nu este de înțeles fără alte cuvinte lămuritoare. Trebuie să se fi avut în vedere modul de exprimare antropomorf, de personificare, propriu alchimiei.
38. ceea ce... s-a și numit regula philosophandi: Newton, în opera sa de căpătâi Phiolosophiae naturalis principia mathematica (1687). La începutul celei de-a treia cărți, în pasajul în care este vorba despre inaugurarea mecanicii cerești, el formulează drept idei călăuzitoare pentru transpunerea mecanicii pământești la cea cerească trei (mai târziu patru) regulas phiolosophandi și dă exemple care coincid în parte exact, în parte cu mici variațiuni, cu cele date aici.
39. putem obține explicații doar: schimbat din „putem obține ceva... în mod elementar”.
40. Pierre Simon Maquis de Laplace, Beaumont-en Auge, Dép Calvádos, 1749–1827, Paris. A desăvârșit în mod grandios mecanica cerească întemeiată de Newton. Mécanique céleste, 5 volume, Paris, 1799–1825. Anterior acestora scrisese lucrarea Exposition du systéme du monde, 1796, fără formule matematice, care atestă și nivelul său de scriitor.
41. Istorie naturală și teoria cerului: apărută anonim în 1755. Scrisă absolut în spiritul natural-științific „din perspectiva mecanicii cerești” a lui Newton. „Dați-mi numai materie, vreau să clădesc din aceasta o lume!” proclamă autorul în introducere.
42. planul ecuatorului solar: se mai obișnuiește să se facă referire la planul eclipticii. Privit sub aspectul genezei teoriei Kant-Laplace, planul ecuatorial solar pare a fi mai important oricum, și în consecință el apare și la Kant. Teoretic, ar fi de așteptat ca cele două plane să se suprapună. Nu acesta este cazul. Ele sunt înclinate unul fată de celălalt cu 7°. Aproape aceeași înclinare o are și planul orbitei planetei cea mai apropiată de Soare, Mercur, însă în rest el nu coincide decât în mare cu cel al ecuatorului solar, în timp ce liniile nodurilor celor două pe ecliptică fac un unghi de 27°, care anual crește cu 8”. Numind aici ecuatorul solar plan de referință, se iau în considerare o mulțime de situații, pe care astronomia trebuie să le preia fără explicație, ca simple fapte: diferențele planelor orbitale unele față de celelalte și diferențele, de cele mai multe ori mari, ale planelor ecuatoriale ale planetelor față de planele orbitale. Pentru Pământ, aceasta este înclinația axei Pământului (de 23,5°), atât de importantă pentru tot ce este viață. Dacă Rudolf Steiner a pus un accent atât de mare pe a treia lege fundamentală a lui Copernic, este sigur că a făcut-o și pentru că ea se situează altfel față de enigma acestei înclinarii decât mecanica cerească. Conform acesteia din urmă trebuie să ne așteptăm ca toate relațiile să fie într-o ordine perfectă, precum la Jupiter, unde orbita planetară, ecuatorul planetar și planele orbitale ale sateliților principali (chiar și ecliptica) diferă foarte puțin între ele. Pentru Pământ nu se întâmplă așa. Că toate acestea nu sunt un simplu joc o arată energia cu care s-a vorbit în această problemă, chiar dacă numai în puține ocazii. A se compara aici, de exemplu, conferința menționată în nota 73.
43. ceea ce au accentuat întotdeauna filosofii: ideea nu a putut fi găsită la filosofii cei mai cunoscuți. Cel mai mult se apropie de ea cei care, declarat sau nu, gândesc mai departe Istoria naturală și teoria cerească a lui Kant. Astfel, Carl du Prel (Istoria evoluției universului. Schiță a unei filosofii a astronomiei, ediția a treia adăugită a lucrării: Lupta pentru existență în cer, Leipzig 1882, p. 166) spune: „Sistemul planetar, ca urmare, este conservativ, cel al cometelor schimbător... Aparenta contradicție, după care gravitația poate aduce cu sine rezultate atât de diferite, este rezolvată de teoria evoluționistă: cele două grupe principale ale sistemului solar se găsesc în stadii diferite ale unui proces de adaptare reciprocă a elementelor componente; în ceea ce privește sistemul planetar, acest proces este încheiat, a ajuns la starea lui de echilibru, din care cauză este conservativ; sistemul cometar, din contră, este schimbător deoarece el nu și-a găsit încă starea de echilibru”.
44. Dacă urmărim lucrurile în continuare, în special la Laplace: o primă demonstrație a stabilității sistemului planetar a fost făcută cu ipoteze simplificatoare de Lagrange. De la el provine și primul exemplu al unei „inflexibilități dinamice” a unor planete, care datorită forțelor de gravitație au o perioadă de revoluție condiționată. (Pe orbita unei planete mari există, la un interval de 60°, așa numitele „puncte Lagrange”, în jurul cărora corpurile mici pot efectua oscilații sau „librații”, numite și puncte de librație.) Ulterior s-a găsit un exemplu pentru așa ceva printre planetoide, în constelația „Troienelor”. Mai nou, punctele Lagrange joacă un rol la sateliții lui Saturn, cercetați mai îndeaproape cu ajutorul sondelor cosmice. – De la Laplace ne-au rămas dezvoltările în serii, pentru rezolvarea prin aproximări a „problemei mai multor corpuri”, din care s-a dedus că în cazul rapoartelor raționale ale perioadelor de revoluție ale planetelor perturbațiile ar trebui să se însumeze, ajungându-se astfel la instabilitate. Mai târziu, o temă de concurs cu premii a Academiei Suedeze a avut ca rezultat o lucrare mare (1885) a lui Poincaré, în care se arăta că seriile despre care era vorba sunt divergente, că deci nu există soluții (generale). Abia în 1963 Arnold a dat soluții concrete, însă doar cu o demonstrație strictă de convergență. În realitate, seriile pomenite nu sunt convergente pentru anumite rapoarte raționale ale perioadelor de revoluție. Însă din cercetările moderne ale teoriei Kolmogoroff-Arnold-Moser (= KAM) rezultă o noțiune de stabilitate nouă, precum și un fel de noțiune de comensurabilitate „practică”. Aceasta din urmă se bazează pe faptul că suma multiplicităților ce intră în discuție trebuie să fie mai mică decât 4. Prima se poate atunci formula cum că orbitele stabile reprezintă „majoritatea covârșitoare”, în sensul teoriei măsurării. – Ideea „stabilității veșnice” își găsește o aplicație practică în cazul perioadelor de revoluție ale particulelor de pe un inel de acumulare al sincrotronului de protoni de la CERN (Geneva). Teoria KAM confirmă – dincolo de orice posibilitate de calcul numeric – posibilitatea ca majoritatea orbitelor, la miliarde de revoluții, să se limiteze la un inel îngust. Lor le-ar corespunde în sistemul planetar timpi care la această scară ar depăși existența admisă a universului. Pe scurt, rezultatele moderne permit să se vorbească de o „incomensurabilitate practică” a rapoartelor perioadelor de revoluție din sistemul planetar drept cauză a stabilității acestuia – până la „împlinirea oarecum a unei veșnicii”, – lucru care este pomenit și în text. Aici, parțial, „stagnarea” poate fi interpretată în sensul inflexibilității dinamice, așa cum există în cazul rotației condiționate a Lunii și a altor sateliți ai planetelor. Asupra acestui lucru se face referire din nou în Conferința a VIII-a. – Un alt indiciu al acestei incomensurabilități reale se poate vedea în golurile pe care le prezintă centura de planetoizi chiar acolo unde există multiplicitate sau rezonanță scăzută în perioadele de revoluție. Planetoizii au fost împinși, așa se spune, pe alte orbite din cauza instabilității lor. (În ce privește teoria KAM, a se compara autoreferatul unei conferințe de Jürgen Moser din „Neuer Züricher Zeitung” din 14.5.1975.)
45. Iar acolo unde... apare o incomensurabilitate..., scriem fracția zecimală: la prima ediție pasajul suna astfel: „Iar acolo unde intervine incomensurabilitate ne aflăm chiar în locul și momentul unde în dezvoltarea matematică trebuie să ne fixăm la un număr incomensurabil. Acolo facem ca numărul propriu-zis să se oprească. Scriem fracția zecimală...”. El a fost modificat în conformitate cu sensul, deoarece este aproape imposibil să stenografiezi corect un pasaj ca acesta fără o înțelegere lucidă. Nu este exclus ca acele cuvinte care au prefixul „in” să se fi amestecat cu cele care nu au prefixul „in”. Din păcate, lipsește stenograma de aici și din pasajul analog din Conferința a VIII-a.
46. Peter Hille, Erwitzen, lângă Paderborn, 1854–1904, Berlin-Lichterfelde.
47. Acest fapt ni-l arată calculul însuși: aceasta este și părerea lui Laplace. După noile investigații din anii '60 menționate, incomensurabilitatea nu este premisa stabilității sistemului. Ea este deci un fenomen independent. Aceasta întărește convingerea exprimată aici, mai ales dacă luăm și cele ce se spun în Conferința a VIII-a. Incomensurabilitatea poate deveni rezultat al observației atunci când nu se găsește un interval de timp după care evenimentul se repetă; a se compara și expunerea care urmează, despre care tocmai am amintit.
48. al ovulului nefecundat: „nefecundat” în loc de „fecundat”, conform stenogramei.
49. panspermie: prin aceasta s-a avut în vedere concepția reprezentată de Darwin și numită „pangenesis” (Charles Darwin, Variația tipurilor de animale și plante în stare domestică, cu suplimentul Ipoteză provizorie a pangenezei, 1868). „Panspermie”, oarecum în sensul lui Svante Arrhenius, are drept conținut împrăștierea și migrarea germenilor de viață în univers.
50. Charles Darwin, Shrewsbury, 1809–1882, Down, lângă Beckenham. Opera sa de căpătâi Nașterea speciilor prin selecție naturală a apărut în 1859.
51. este tot atât de puțin apropiat: „puțin”, a fost adăugat.
52. numărul incomensurabil dincoace (în astronomie): „numărul incomensurabil”, pus în loc de „dincolo de numărul incomensurabil”.
53. ceva asemănător cu geometria: în stenogramă apare „care este geneza numărului”.
54. Ernst Blümel, Viena, 1884–1952. Matematician. Profesor la școala liberă Waldorf și la alte școli. De la el provine – foarte probabil, judecând după formulele și corecturile scrise de mână – o redactare completă a textului pentru cursul de față. Pe aceasta editorii au primit-o într-o fază înaintată de lucru, așa încât ea nu a avut nici o influență asupra textului. În afară de copia-Hummel, nu pare să mai fi stat o altă documentatie la baza textului. Probabil elaborarea este premergătoare primei ediții, în orice caz fără să o influențeze.
55. aceasta nu este o axiomă, ci un postulat. Vezi aici nota de la p. 24, vol. III, p. IX din Introducerile la scrierile de științe ale naturii ale lui Goethe.
56. Ernst Haeckel, Potsdam, 1834–1919, Jena. Zoolog.
    
    Oscar Hertwig, Friedberg, Hessen, 1849–1922, Berlin. Anatomist.
57. mai întâi se presupune ceva diferit: „diferit”, este completat.
58. în forme și raporturi: „forme”, modificat din „formule”.
59. Enigmele sufletului, GA 21, O.C.
60. Unii dintre dumneavoastră știu deja...: participanții la primul curs de științe naturale. A se compara Impulsuri spiritual-științifice pentru dezvoltarea fizicii. Primul curs de științe naturale, GA 320, O.C., 1964, p. 126.
61. suntem foarte legați de lume în răstimpul dintre momentele...: în loc de „cât de mult depind intervalele de timp”.
62. În cartea mea Știința ocultă am arătat...: Știința ocultă în rezumat (GA 13), 1977, pp. 63–64 și p. 418.
63. căci, în definitiv, diversele sisteme cosmice sunt ceva haotic: „diversele”, completat conform paragrafului de mai sus.
64. numim... proces de cunoaștere: „proces de cunoaștere” în loc de „proces de clarificare”, conform copiei.
65. să interpreteze... istoria biblică a Creației prin realități embriologice: Se spune că este vorba de tradiții, deci nu de embriologie în sens naturalist-științific. H.P. Blavatsky, în Isis dezvăluită (vol. 1, ediție germană, Leipzig, fără an, p. 388) face referire la concepții cabalistice despre armonie între evoluția embrionară și cea cosmică, ce-i drept fără indicarea unei anumite literaturi. Privitor la embriologia ocultă din scrierile alchimiste, a se compara observația lui Rudolf Steiner din prima conferință a ciclului: Locașuri și misterii ale Evului Mediu (GA 233a), 1980, p. 26.
66. dictonul nietzschean: din Cântec de pahar, partea a 4-a de la Așa grăit-a Zarathustra.
67. Enigmele filosofiei (GA 18),1968, capitolul 5, p. 91.
68. sunteți conduși înapoi până la un punct de cotitură: „până la un punct de cotitură” este adăugat, în sprijinul celor spuse la începutul capitolului următor.
69. despre realism și nominalism: a se compara cu lucrarea care tocmai a fost menționată: Enigmele filosofiei, p. 94 sau Filosofie și antroposofie (GA 35), 1965, p. 89.
70. așa-numita demonstrație ontologică a existenței lui Dumnezeu: se referă la cea a lui Anselm de Canterbury (1033–1109). Privitor la aceasta, a se vedea lucrarea menționată mai sus, Enigmele filosofiei, p. 94.
71. Vincenz Knauer, Viena, 1828–1894, Viena. Teolog catolic, conferențiar la Universitatea din Viena.
72. și în ei s-a cuibărit ceva ce a pus spiritul...: „în ei s-a cuibărit ceva” este adăugat.
73. apogeul epocilor glaciare: așa cum se poate deduce din cartea Cursul vieții mele (GA 28, 1982, p. 48), Rudolf Steiner a primit imboldul de a se ocupa cu epoca glaciară încă de la sfârșitul perioadei sale școlare, datorită articolului profesorului său Franz Kofler, interes care l-a însoțit pe parcursul întregii vieți. Articolul lui Kofler se bazează pe explicația astronomică a glaciațiunii, dată de A.J. Adhémar (Révolutions de la mer, Paris, 1842, ediția a 3-a, 1874). El a apărut în anul 1879 în darea de seamă anuală nr. 14 a școlii medii reale de stat Wiener-Neustadt, partea de jos a Austriei, iar în 1927 a fost făcut din nou accesibil cititorilor prin intermediul lui C.S. Picht, într-o apariție privată. Zece ani după ce se îndeletnicise cu acest articol, Rudolf Steiner a scris rubrica „Glaciațiune” din dicționarul enciclopedic Pierer (ed. a 7-a, editat de Joseph Kürscher, Berlin și Stuttgart 1889). Drept cauze principale ale glaciațiunii sunt indicate aici schimbările intervenite în distribuția apei și uscatului și în durata anotimpului de iarnă. Conform legii a doua a lui Kepler, iarna este lungă atunci când Pământul, iarna, trece prin afeliu și scurtă în situația opusă. Aceste condiții se schimbă la perioade de 21 000 de ani. O influență mai au aici, desigur, și variațiile de excentricitate ale orbitei Pământului și înclinația axei acestuia, care, mai ales dacă sunt periodice, se întind pe perioade de timp și mai mari. În timp ce aceste din urmă influențe sunt dezbătute foarte amănunțit la Kofler, în rubrica din dicționarul enciclopedic ele sunt atinse doar pe scurt, iar în cursul de față nu sunt menționate direct. A se compara în legătură cu articolul și cu rubrica din dicționarul enciclopedic, precum și cu problema glaciațiunii în general, cartea semnată de Elisabeth Vreede, Astronomie și antroposofie, Dornach 1980, pp. 360–389. Problema glaciațiunii funcție de poziția axei Pământului este tratată direct din punct de vedere spiritual în conferința din 31.12.1910, din volumul Istorie ocultă (GA 126).
74. Am arătat aceasta adesea în conferințele antroposofice: De exemplu în lucrarea Conducerea spirituală a omului și omenirii (GA 15, p. 57), care redă conferințele din anul 1911 într-o formă revizuită.
75. Aristotel, 384–322 î.Hr. Discipol al lui Platon și dascăl al lui Alexandru cel Mare.
    
    Platon, 427–347 î.Hr., a trăit în Atena. Discipol al lui Socrate. A întemeiat în dumbrava Academos școala sa, punctul de pornire al tuturor „academiilor”.
    
    Heraclit, aproximativ 540–480 î.Hr., a activat în Efes.
76. găsiți în cartea mea Știința ocultă: la p. 282, vezi nota 62.
77. nuanțării lingvistice a culorii albastru: O expunere anterioară se găsește în conferința publică ținută în 24.3.1920 în Basel, care deocamdată este tipărită doar în revista „Menschenschule”, anul 13 de apariție, Basel 1939, p. 256.
78. clima tropicală s-a instalat... în India: a se vedea conferința Culturile preistorice și timpurii ale Europei și Asiei (în GA 325), 1969.
79. Am explicat deja asta: în Conferința a II-a.
80. V-am descris această acțiune... care la copil acționează: în Conferința a III-a.
81. un fapt pe care l-am evidențiat deja adesea: de exemplu, în conferințele Corespondențe între microcosmos și macrocosmos. Omul – o hieroglifă a universului (GA 201), conferințele 4, 12 și 14.
82. așa cum am mai menționat deja adesea: în conferințele pomenite în nota precedentă.
83. două surse sonore: „surse sonore” în loc de „unde sonore”, conform stenogramei.
84. a te deplasa... cu o viteză mai mare ca a sunetului: despre acest lucru, conferința din 21.8.1916, în Enigma omului (GA 170) vorbește mai pe larg. Faptul că nu este vorba de un mic amănunt s-a arătat în ultimele decenii prin apariția „pragului sonic”, care se poate depăși și care, pentru gândirea ruptă de realitate, nu se poate depăși.
85. cum am descris condițiile de pe vechea Atlantidă: în cartea Din Cronica Akasha (GA 11), în capitolul „Strămoșii noștri atlanteeni”.
86. în sensul mai abstract în care s-a exprimat Kirchhoff mai târziu: În prefața cărții sale Mecanica (Prelegeri despre fizică-matematică. Mecanica, Leipzig 1876) spune: „Se obișnuiește a se defini mecanica drept știința care se ocupă cu forțele, iar forțele drept cauzele care provoacă mișcările sau tind să le provoace... Acestei definiții însă îi este inerentă ambiguitatea, de care noțiunile de cauză și tendință nu sunt scutite... De aceea eu consider că obligația mecanicii este să descrie mișcările care au loc în natură, și anume să facă acest lucru în modul cel mai simplu și mai complet. Cu aceasta vreau să spun că aici este vorba de a arăta care sunt fenomenele care au loc, nu însă a determina și cauzele lor”. Cartea lui Kirchhoff este o mărturie a faptului că toată mecanica se dezvoltă conform acestei atitudini.
    
    Gustav Robert Kirchhoff, Konigsberg, 1824–1887, Berlin.
87. într-o fiziologie a simțurilor, care le tratează pe toate global: „global” în loc de „al lor”.
88. foronomia este un alt exemplu: copia are aici și, în frazele care urmează, în loc de „foronomie” și „foronomic”, cuvintele „embriologie” respectiv „geometric” sau chiar „fiziologic”.
89. o pornim de la alte structuri: „structuri” în loc de „domenii”, conform stenogramei.
90. să se extindă această teorie evoluționistă și asupra astronomiei; Carl du Prel a scris o Istorie a evoluției universului (Leipzig 1882), care este a treia ediție a lucrării Lupta pentru existență în cer; a se compara cu nota 43. H. Lotze avansează astfel de idei în cartea sa Microcosmos și face aproximativ următoarea descriere (p. 29): „Realitatea însă, din numărul infinit al combinațiilor elementelor pe care le putea oferi un haos lipsit de rațiune, nu conține o selecție pe care s-o fi creat intenționat o anumită voință, ci suma mai mică a acelor structuri, pe care însuși mersul mecanic al naturii le-a verificat în nesfârșita alternare a evenimentelor sale și le-a separat – ca pe un întreg, apt în sine de a fi conservat – de pleava zburătăcită a ceea ce este haotic, căreia el însuși, imparțial, i-a dat naștere și pe care tot el, la fel de imparțial, a făcut-o să dispară” (ed. a 4-a, Leipzig, 1885).
91. structură solar-planetară: conform stenogramei, în loc de „sistem solar-planetar”.
92. Hermann Minkowski, Alexota, lângă Kowno, 1864–1909, Göttingen. În 1909 a ținut conferința Spațiu și timp.
93. celelalte conferințe: patru conferințe pe jumătate publice pentru absolvenți universitari, Mărturii asupra relațiilor științei spiritului cu diferite domenii ale științei, 11-15 ianuarie 1921, apărute în revista „Gegenwart”, anul 14 de apariție, Berna, 1952/1953.
94. școala Waldorf: școala liberă Waldorf, Stuttgart, întemeiată în 1919 de Emil Molt (1876–1936) pentru copiii de muncitori ai fabricii de țigarete Waldorf-Astoria și pentru copii în general. Școală unitară, cu curs gimnazial și liceal, condusă de către Ruolf Steiner până la moartea sa, în anul 1925.
95. întrebările... în legătură cu cele expuse: răspunsul la întrebări a fost dat la sfârșitul ultimei conferințe.
96. V-am atras atenția că aceste numere care reprezintă rapoartele... sunt mărimi incomensurabile: Conferința a IV-a și apoi Conferința a VIII-a și Conferința a XVIII-a.
97. epoca de cultură protohindusă: vezi Știința ocultă, nota 62, p. 272.
98. tocmai prin prezența aici a viețuirii senzoriale: „viețuire senzorială” în loc de „rezultatul simțurilor”, conform stenogramei.
99. în vechiul tărâm atlantean: vezi nota 85.
100. în conformitate cu un anumit liber-arbitru: „liber-arbitru” în loc de „cultură a voinței”, conform stenogramei.
101. un reactiv pentru aprecierea fenomenelor cerești: „fenomene cerești” în loc de „fenomene cosmice”, conform stenogramei.
102. planta perenă nu poate să ne spună prea multe în această privință: introdus „prea multe” în loc de „mult mai mult”.
103. în sistemul planetar ar fi luat naștere perturbații, care... ar fi adus sistemul planetar la starea de repaus: a se compara aici a, b, c astronomic-Brockhaus, Leipzig 1977, articolul „Sistemul solar”: „Datorită perturbațiilor permanente pe care le provoacă planetele mari, în primul rând masivul Jupiter, asupra orbitelor corpurilor aflate în cea mai mare parte de timp în apropierea lor, respectiv în părțile interioare ale sistemului solar, se creează relații strânse între orbitele lor și orbitele planetelor. Astfel de legături există între orbitele planetoidelor și orbita lui Jupiter și între orbitele cometelor cu perioadă scurtă de revenire și unele orbite planetare”. Iar în articolul „Planetoidele”: „Astfel numeroase planetoide au aproximativ aceeași distanță la periheliu ca și Jupiter”. În acest context, „repaus” ar echivala cu comensurabilitate, adică cu perpetua revenire la situația anterioară.
104. se poate demonstra printr-un calcul simplu: comensurabilitate este echivalent cu a spune că toate rapoartele sunt expresii de numere întregi. Calculul ar decurge atunci astfel: scriem toate rapoartele ca fracții și apoi le aducem la același numitor. Acesta indică timpul după care tot procesul a ajuns din nou în punctul inițial de pornire. Un astfel de timp nu există la rapoartele incomensurabile.
105. Această situație o calculăm de fapt... În acest caz ne apropiem...: schimbat din „Această situație o calculăm de fapt, căci, dacă am ajuns la sfârșitul calculului, am ajuns la incomensurabil; aici ajungem...”, conform primei ediții. A se compara pasajul din Conferința a IV-a și nota 45.
106. Dacă luăm în considerare doar forța de gravitație..., vom ajunge... la raportul comensurabil: acest lucru se vede ori de câte ori forța de gravitație este mare. De exemplu, pentru perioadele de revoluție ale sateliților principali ai lui Jupiter. Chiar și lui Laplace îi era cunoscut că există următorul raport de numere: rotația medie a primului satelit plus de două ori rotația celui de-al treilea este egală exact cu triplul rotației celui de-al doilea. Mai mult, sateliții prezintă față de Jupiter mereu aceeași față. La fel se întâmplă cu Luna față de Pământ. Același lucru se presupune și pentru sateliții care evoluează cel mai aproape în jurul lui Saturn, cu toate că este dificil de confirmat. Și aici este valabilă o comensurabilitate asemănătoare cu a lui Jupiter: rotația medie a lui Tetis, plus de patru ori cea a lui Dione, plus de cinci ori cea a lui Mimas este egală cu de zece ori rotația medie a lui Enceladus. Pentru Mercur, aflat cel mai aproape de Soare, până acum un deceniu și jumătate se presupunea, de asemenea, că ar avea îndreptată mereu aceeași față spre Soare. Acest lucru nu s-a confirmat, ce-i drept, însă s-a confirmat următoarea comensurabilitate: la trei rotații ale lui Mercur în jurul axei sale se fac două rotații în jurul Soarelui. A se compara nota 134 (Conf. Gilbert E. Satterthwaite, Encyclopedia of Astronomy, Londra 1970, și Encyclopedia Britannica, Knowledge in Depth, 1974, articolul „Saturn, Jupiter și Mercur”).
107. ce se comportă invers: „invers” în loc de „divers”, conform stenogramei.
108. Iar Hegel nu putea ignora un astfel de subiect: cugetarea sa despre comete și anii buni pentru vin se găsește în Enciclopedia științei filosofice în rezumat, partea a doua, Filosofia naturii, editată de Carl Ludwig Michelet, 1847, p. 154.
     
     Georg Wilhelm Friedrich Hegel, Stuttgart, 1770–1831, Berlin.
109. atâtea comete câți pești... în mare: Johannes Kepler, „Raport amănunțit despre recent apăruta cometă” [din anul 1607], Hall, în Saxonia 1608. Studiul începe cu cuvintele: „Părerea mea simplă despre comete este că, așa cum o buruiană, o iarbă iese în mod natural din orice Pământ, chiar și fără semințe, iar în orice apă, în mările largi cresc pești și plutesc în ea din abundență, cum deci și marea întindere care este oceanul nu rămâne în nici un caz goală, ci din plăcerea deosebită a lui Dumnezeu-Creatorul balenele cele mari și alte minuni ale mării o populează și cutreieră în lung și în lat intinderile ei vaste, întru totul asemănător stau lucrurile și cu aerul liber din văzduh, care se întinde peste tot, adică poate avea această calitate de a naște din sine și comete, pentru ca oricât de mult s-ar întinde el să fie străbătut în orice colțișor de comete și deci să nu rămână în nici un caz gol... Cerul, după mine, conține în el atâtea comete câți pești are marea”. Astăzi se estimează la 10¹⁰ numărul cometelor din sistemul solar (a, b, c astronomic-Brockhaus, rubrica „Sistemul solar”, Leipzig 1977, p. 372).
110. cursul despre teoria căldurii: Impulsuri spiritual-științifice pentru dezvoltarea fizicii. Cursul doi de științe naturale (GA 321), sfârșitul conferinței 11 și conferința 12.
111. privim curbele uzuale într-o anumită legătură: o primă examinare de acest fel a curbelor adunării, scăderii, înmulțirii și împărțirii se găsește în conferința a treia (din 28 iunie 1914) din lucrarea Căi spre un stil arhitectural nou (GA 286). Se știe că auditoriul a fost foarte surprins, în cadrul acelor expuneri artistice care se adresau participanților la ridicarea clădirii primului Goetheanum, să urmărească o conferință de matematicâ. Abia mult după moartea lui Rudolf Steiner, Carl Kemper și-a dat seama, tocmai datorită acestei conferințe, că la baza planului de clădire stă cercul împărțirii, cu raportul de divizare 1 : 3, astfel încât conferința matematică din cadrul ciclului Căi spre un stil arhitectural nou și-a aflat dintr-odată rațiunea. Anterior exista o cu totul altă părere în ceea ce privește planul de clădire. Conferința mai conține și explicații detaliate despre curbele lui Cassini și formele lor. Prezentarea acestor curbe în cursul de față este strâns legată de manualul lui Lübsen (Heinrich Borchert Lübsen, Manual detaliat de geometrie analitică sau superioară pentru studiul individual, ediția a 11-a 1876). Această ediție și edițiile anterioare ale cărții nu se află în biblioteca lui Rudolf Steiner. Din autobiografia Cursul vieții mele (GA 28, p. 42) se știe însă ce importanță se acorda în școală pe vremea lui Rudolf Steiner cărților de matematică ale lui Lübsen. Aceste ediții vechi nu au nici o tangență cu ideea de sistematizare a curbelor în funcție de cele patru operații aritmetice. Cercul împărțirii lipsește complet. Ideea de sistematizare apare însă în lucrarea revizuită prin intermediul lui A. Donadt (ediția a 15-a, 1908), din care există un exemplar al ediției ulterioare, din 1919, în biblioteca lui Rudolf Steiner, însă – curios – cu paginile netăiate la paragraful respectiv. Chiar dacă pare de la sine înțeles a trata împreună curbele celor patru operații matematice de bază, în literatura matematică această idee nu se găsește totuși, căci nimeni, de altfel, nu face cu plăcere o legătură între curba lui Cassini și celelalte trei curbe, mult mai simple.
112. curbă a lui Cassini: în contextul de față este foarte interesant că această curbă s-a născut din considerente pur astronomice, și anume ca orbită a Soarelui. Acest lucru îl dovedește fiul, Jaques Cassini (în Eléments d'astronomie, Paris 1740, pp. 149–151). Printre numeroasele tratate ale descoperitorului însuși, Giovanni Domenico Cassini (Nissa 1625–1712, Paris), nu s-a găsit nici unul care să dea o explicație mai în detaliu asupra curbei. Pare să nici nu fi știut cum a ajuns la curba înmulțirii. Deja în 1755, D'Alambert a fost însărcinat să emită o presupunere despre aceasta (în vol. 5 al enciclopediei lui Diderot, articolul „Elipsă. Elipsa lui M. Cassini”). Cassini este probabil să fi fost interesat exclusiv de forma elipsică. Pe căile trasate de Rudolf Steiner pentru dezvoltarea științei, curbei lui Cassini i se acordă o importanță deosebită. La congresul filosofilor de la Bologna din 1911, el o prezintă ca un exemplu important pentru un conținut mediativ, prin care să se încerce lărgirea conștienței, în scopul unei cunoașteri suprasensibile (Filosofie și antroposofie GA 35, 1965, p. 118).
113. Când avansez pe această porțiune (de la 1 la 2): paranteza este interpretarea editorului pentru cuvântul „această”. Figura care a fost dată nu conține cifre.
114. să privesc cealaltă ramură ca pe ceva izolat în sine: „izolat” a fost adăugat.
115. obținem forme diferite ale cercului: deosebirea de formă constă aici în curbura acestuia.
116. Puteți urmări aceasta în ecuație. Cercul devine însăși axa ordonatelor: în caietul de notițe nr. 52 (1921), această urmărire este efectuată în felul următor:
     [(x − a)² + y²]^½ : [(x + a)² + y²]^½ = m : n
     (n² − m²) ∙ x² + (n² − m²) ∙ y² − 2a (n² + m²) ∙ x + (n² − m²) ∙ a² = 0
     Centrul are coordonatele: a ∙ (n² + m²) : (n² − m²), 0
     r = a ∙ 2mn : (n² − m²)                      m = n − ecuația ordonatei
     (Din motive de redactare aici s-a pus în loc de linie de fracție semnul de împărțire și în loc de rădăcină pătrată exponentul 1/2.)
117. Desigur că nu am cum să desenez acest cerc: interiorul său nu se poate densa, căci ar ajunge la infinit; conturul lui se poate trasa ca un cerc obisnuit.
118. Ernst Blümel: vezi nota 54.
     
     Herman v. Baravalle, Viena, 1898–1973, Wiesneck. Matematician, pedagog de matematică și fizică, autor de manuale, profesor la școala Waldorf și fondator al unor școli corespunzătoare în SUA.
119. Carl Unger, Bad Cannstadt, Stuttgart, 1878–1929, Nürnberg. Dr. ing., proprietar și director al unei uzine mecanice. Epistemolog. Membru în colegiul director al Societății antroposofice.
120. traseul unui punct... pentru ca în alt punct... B... să aibă mereu aceeași străucire: în Geometrie superioară de Lübsen (compară nota la „curbele uzuale”), această proprietate a curbei lui Cassini este menționată într-o notă de subsol, fără o explicație mai amănunțită. – Dacă un punct M propagă o undă, care vine din A, conform principiului lui Huygens, respectiv izotrop și proporțional cu intensitatea care ajunge la el, acesta trebuie să descrie de fapt o curbă Cassini, pentru ca unda secundară care pleacă de la el să ajungă în B cu o intensitate constantă. În cazul strălucirii luminii, acest lucru s-ar întâmpla dacă ar exista particule care să se propage izotrop.
121. pe marginea cursului pentru medici, ținut la Dornach: ciclul de conferințe Corespondențe între microcosmos și macrocosmos, îndeosebi conferința nr. 2, vezi nota 81.
122. un fel de spectru inversat, pe care Goethe l-a ordonat de asemenea: vezi primul și al doilea curs de științe naturale, Impulsuri spiritual-științifice pentru dezvoltarea fizicii (GA 320 și GA 321), în special conferința a 4-a respectiv conferințele 8, 9 și 11. În fig. 12 s-a adăugat „albastru” și „galben”, ca părți exterioare ale spectrului inversat. Aici este vorba doar de partea interioară. Dacă ea se pune, ca la prima ediție, singură în dreapta, în prelungirea fig. 11, astfel încât cele două culori violet să se învecineze, ia naștere, ideal, figura închisă de forma unei drepte, care se închide peste punctul de la infinit (roșu). Atunci galben și albastru sunt comune ambelor spectre.
123. în institutul nostru de fizică urmează să fie făcut unul din primele montaje experimentale: acesta a fost pus la punct în Institutul de cercetări din Stuttgart, pe vremea celui de-al doilea curs de științe naturale. Curând după aceea el a căzut pradă incendiului din anii '20. În ciuda primului rezultat pozitiv, experimentele nu au fost încheiate. Mai târziu nu s-a mai ivit ocazia realizării condițiilor, foarte exigente, de experimentare din anii '20.
124. Enigmele sufletului: vezi nota 59.
125. V-am atras atenția...că, de fapt, principiul metamorfozei ar trebui să fie modificat: Conferința I.
126. sfera cerească față de raza terestră: „raza terestră”, în loc de „activitate a Pământului”, conform stenogramei.
127. constituie oarecum două unilateralități: „constituie” în loc de „construiesc”, conform stenogramei.
128. sistemul ritmic: „sistemul” în loc de „domeniul”, conform stenogramei.
129. cu organizarea noastră omenească: „organizarea omenească” în loc de „organizare a lumii”, conform stenogramei.
130. se aplică... prin neglijarea fazelor de oscilație: se aveau în vedere formulele lui Fresnel, care exprimă ce cantitate dintr-o undă de lumină care cade pe un mediu optic mai dens este reflectată la suprafața de separare și ce cantitate pătrunde mai departe, cu schimbarea direcției. Aici reflexia se face cu un salt de fază de o jumătate de perioadă. Fresnel a obținut formulele pe cale mecanică, respectiv din teoria elastică a luminii. În teoria electromagnetică actuală a propagării luminii, valabilitatea lor a rămas neschimbată.
131. modul de gândire specific mecanicii... care... are de-a face cu forțe centrale: în conferința întâi din primul curs de științe naturale (Impulsuri spiritual-științifice pentru dezvoltarea fizicii. Primul curs de științe naturale, GA 320, O.C.) s-a explicat opoziția dintre forțele centrale cu potențial și forțele universale fără potențial. Pasajul de față le definește pe acestea din urmă prin mișcări rotitoare, de forfecare și de deformare. În mod analog a caracterizat Eduard v. Hartmann „supraforțele organice” ale sale. Rudolf Steiner le-a menționat pe acestea din urmă în conferința publică din 12.11.1917 (Completarea științelor actuale prin antroposofie, GA 73, O.C., 1973, p. 124). Ca un cunoscător profund al științelor naturii, Hartmann și-a dat seama că acestea nu pot evita forțele care transcend forțele centrale. El le descrie în Sistem al filosofiei în rezumat, vol. 2, Compendiu de filosofie a naturii (1907), p. 213 prin cuvinte precum cele ce urmează: „Supraforțele organice în primul rând nu sunt forțe materiale, mecanice, energetice..., în al doilea rând nu sunt inteligențe conștiente..., în al treilea rând nu sunt individuale... Supraforțele organice acționează în primul rând curbiliniu (nu rectiliniu), rotitor, forfecător sau deformator. . . , în al doilea rând desfășoară o inteligență supraconștientă. . . , în al treilea rând sunt supraindividuale. .. Există supraforțe organice ale organelor celulare, ale celulei..., ale regnurilor naturii, ale corpurilor cerești și ale universului”. A se compara și cu nota la p. 301.
132. în urmă cu circa 50 000 de ani: figurile 2 și 3, împreună cu indicația de 50 000 de ani se află în cartea lui A. Disterweg, Astronomie populară, ediția a 2-a, 1904, p. 346, care a cunoscut o largă răspândire. Lucrări de informare mai recente precum Lexiconul Meyer (1972) sau a, b, c astronomic Brockhaus (1977) conțin cam aceleași figuri, însă cu indicația de 100 000 de ani.
133. deplasările stelelor pe direcția liniei de vizualizare: asupra acestui lucru se va reveni în Conferința a XVI-a.
134. Ulterior însă ea se întoarce... după care își continuă drumul mai departe: expunerea despre Mercur care urmează după aceste cuvinte a fost redată în prima ediție sub următoarea formă modificată: „El face o dată astfel de bucle în timpul unei perioade de revoluție sinodică (fig. 4). Este ceea ce pentru observație noi putem numi, în prima instanță, mișcarea planetei Mercur. Restul traiectoriei este simplu, doar că în unele locuri prezintă aceste bucle”. Această modificare corespunde astronomiei elementare. O notă din caietul de notițe din perioada cursului (caietul de notițe nr. 52), care este legată de figurile privitoare la formarea buclelor, înregistrează chiar acest aspect al problemei prin următoarele cuvinte: „O buclă în perioada de revoluție sinodică. Pentru Mercur Venus la conjuncția inferioară”. Ceea ce s-a spus însă ulterior la cursul propriu-zis prezintă un cu totul alt aspect, și anume acela care abia prin noile cercetări despre durata de rotație a planetei a intrat atât de mult în conștiență. Despre aceasta s-au spus deja câteva lucruri în observația preliminară, la note. Ar mai fi de adăugat că noile cercetări în ce privește rotația planetei Mercur, făcute prin observații cu ajutorul radarului, arată că durata rotației ajunge la 2/3 din perioada de revoluție siderală de 88 de zile, în timp ce Schiaparelli, în anii '80 ai secolului trecut, credea că a putut stabili, prin observații îndelungate, că Mercur își îndreaptă mereu aceeași față către Soare, asemănător Lunii față de Pământ. De aici rezultă că Mercur, de fiecare dată când este aproape de Pământ, prezintă și față de acesta aceeași față, însă opusă aceleia care o îndreaptă spre Soare. Conform investigațiilor actuale, se pare că nu așa s-ar petrece lucrurile, că Mercur abia la a treia apropiere de Pământ își îndreaptă aceeași față către el. Faptul că aceasta a scăpat observației înseamnă că doar a treia apropiere de Pământ era observată. Celelalte erau prea incomode pentru observațiile și așa destul de dificile. Această diferențiere din cadrul buclelor lui Mercur era atât de puțin prezentă în conștiența astronomilor, încât în manuale și compendii nu s-a putut găsi nimic în această privință. În schimb, un participant la curs, dr. Hermann v. Baravalle, s-a apropiat foarte mult de înțelegerea realității, atunci când în 1938 a schițat în „Calendarul stelar” al secțiunii de matematică-astronomie de pe lângă Goetheanum curba pozițiilor lui Mercur în raport cu Soarele care apune și cu cel care răsare și a notat timpii favorabili de observație pentru aceasta. A lipsit doar formularea explicită a regulii, și anume aceea că într-un an există în principal o buclă favorabilă pentru observare seara și o alta favorabilă pentru observare dimineața.
135. figurile 4–7: forma buclelor, care poate părea nefamiliară, se transformă imediat în forme familiare, dacă inversăm stânga cu dreapta. În acest caz și săgețile vor indica sensul direct (dreapta, sau sensul acelor de ceasornic, n.t.). Inversarea sensului de rotație are niște motive despre care nu se spune nimic. Aceasta apare de asemenea și în euritmie în prezentarea celor „12 dispoziții zodiacale”, unde Soarele, pentru fiecare din cele 12 strofe, parcurge întregul zodiac. Acesta este orânduit în sensul mișcării acelor de ceasornic și tot astfel se deplasează pe scenă și Soarele (compară Nașterea și dezvoltarea euritmiei GA 277a, 1982, p. 70). Când Rudolf Steiner a fost întrebat la o repetiție de euritmie în legătură cu acest sens de rotație, el a răspuns că acesta așa trebuie să fie, deoarece este vorba de o reflectare, o oglindire (comunicare a Ilonei Schubert). În legătură cu aceasta ar mai fi de indicat reflectarea sub care lumea astrală prezintă toate lucrurile și procesele; a se compara eventual și cu În fața porții teosofiei (GA 95), conferința a 2-a.
136. o lemniscată, care la partea inferioară se deschide: în loc de „pornește în jos”.
137. Moriz Benedikt, Eisenstadt, 1835–1920, Viena. Medic, criminalist antropolog.
138. în înseși structurile matematice, în configurațiile geometrice: „structuri”, în loc de „domenii”, conform stenogramei.
139. acolo doar ca imagini aparente: „doar” în loc de „sus”, conform copiei.
140. figura 1: ea trebuie înțeleasă în sensul că bucla se află într-un plan perpendicular pe rază.
141. în astronomia misterială din vechime... se vorbea... de trei Sori: acest lucru îl confirmă Julian Apostatul în Discurs despre Regele Soare (compară Anna Margaret Derbe, Metamorfoză în devenirea istorică, Stuttgart 1979, p. 39). H.P. Blavatsky în Doctrina ocultă, vol. 3, cap. XXIII, insistă atât asupra acestei concepții, în general, cât și asupra reprezentantului acesteia, Iulian Apostatul. A se compara și cu conferința din 24.4.1922, ținută după cursul de față la Londra, în ciclul Misterul solar și misterul morții și învierii (GA 211).
142. și astronomia actuală are trei Sori: o expunere mai exactă se găsește în Conferința a XVII-a.
143. printr-o... combinație a structurii minerale să obțină structura vegetală: „să obțină” este adăugat.
144. generatio aequivoca: sinonim cu „generație spontanee”.
145. un proces de bifurcare: acest fel de proces și punctul ideal apar deja în Scrierile de științe naturale ale lui Goethe. Vezi aici nota de la p. 24, vol. I, p. 11 și observația de acolo.
146. Emil Selenka, Braunschweig,1842–1902, München. Zoolog.
147. citat din Arhimede: Rudolf Steiner a atribuit citatul lui Plutarh. Pasajul se află însă chiar în Calculul nisipului al lui Arhimede. Dacă și Plutarh l-a reprodus nu s-a putut stabili. Probabil există o confuzie cu o altă mențiune a lui Aristarh, prin intermediul lui Plutarh. În această privință Rudolf Wolf (Manual de astronomie, vol. 1, Zurich 1890, p. 536) spune: „În completarea relatării lui Arhimede trebuie amintit că Plutarh, în lucrarea sa De facie in orbe lunae, povestește că s-ar fi gândit să cheme în judecată pe Aristarh din Samos sub învinuirea că disprețuiește religia, deoarece acesta mută focarul sacru al lumii și, «pentru a corecta fenomenul ceresc, consideră cerul fix și, în schimb, Pământul rostogolindu-se pe un cerc înclinat și în același timp rotindu-se în jurul propriei axe»”.
     
     Aristarh din Samos a trăit în jurul anilor 320–250 î.Hr.
     
     Arhimede a trăit în Siracuza între 287–212 î.Hr. Matematician și fizician important. În Calculul nisipului el spune că numărul firelor de nisip pe care l-ar putea cuprinde universul lui Aristarh, exprimat în termeni moderni, ar fi de 10⁶³.
     
     Plutarh, 46–120, scriitor grec, platonician, preot la Delfi. De la el ne-a rămas o operă literară vastă, care dă explicații bogate despre personalități și concepții ale antichității.
148. celei de a cincea perioade de cultură postatlanteană: vezi nota 97.
149. ceea ce este valabil pentru acest Aristarh din Samos a fost valabil și pentru mulți alți oameni: se spune că acest lucru ar fi greu de dovedit prin documente exterioare. Citatul lui Plutarh de mai sus arată cum anumite forțe acționau pentru a nu permite ca asemenea concepții să se răspândească. Cu toate acestea au existat rămășițe ale acestei concepții în primul rând la pitagoricieni, în cercuri restrânse. Acolo se învăța despre rotația Pământului în jurul propriei lui axe și mișcarea lui în jurul unui „focar central”. Deci un Pământ în mișcare de rotație nu este o idee imposibilă pentru greci. Aceasta o întâlnim la Platon. În cărțile de istorie a astronomiei se poate citi că el a ridicat problema reprezentării mișcării circulare uniforme, rezolvată de Eudoxos și Aristotel prin construcțiile lor magistrale de sfere homocentrice. Totuși R. Wolf relatează (p. 211) referitor la el: „Dacă Aristarh... a urmărit în continuare ideile, pe care chiar Platon le-a exprimat timid parțial în Timaios, unde indică rotirea axei pământești, parțial în scrierile de la o vârstă mai înaintată când, conform lui Plutrah, «nu mai consideră Pământul ca fiind centrul Universului, ci acest loc îl cedează unui alt astru mai bun», aceasta nu se mai știe”. În continuare, Wolf face observația că, de asemenea, n-ar fi fost necunoscut faptul că „vechii egipteni considerau planetele inferioare a fi sateliți ai Soarelui”. Exact acest lucru îl afirmă deci, ce-i drept fără a se face însă referire la egipteni, discipolul lui Platon, Heraclid din Pont. Da, dar acesta pare să fi mers și mai departe. La rubrica „Astronomie” din Enciclopedia italiană, care se bazează pe cercetările lui Schiaparelli, se arată că pe vremea lui Heraclid, datorită propriilor lui idei sau ale altora, și planetele superioare erau considerate sateliți ai Soarelui, astfel că sistemul lui Tycho Brahe ar fi fost conceput încă de pe atunci. Heraclid ar fi făcut chiar și următorul pas – propriu-zis heliocentric. Așa se relatează într-un fragment transmis posterității de către Simplicius care, ce-i drept, se încurca în niște controverse filologice. – Curând după Aristarh, caldeeanul Seleukos din Seleukia a demonstrat ideea aceasta, elaborată mai întâi ipotetic de el. După aceea, timp de secole, ea își pierde urma.
150. Claudius Ptolemeu a trăit între 138–180 în Alexandria. Opera sa de căpătâi, numită de către arabi Almagest, dezvoltă într-o imagine de ansamblu sistematică, bazându-se în principal pe Hipparh, astronomia elaborată de către greci.
151. de aici compuneau aceste mișcări: „compuneau” în loc de „adunau împreună”, conform stenogramei.
152. aceste două curbe nu se deosebesc deloc: s-a observat în diferite feluri că construcțiile ptolemeilor, realizate geometric, sunt începutul celor date pe cale analitică de mecanica cerească, prin dezvoltările în serie.
153. Regele Alfons: Alfons al X-lea de Castilia, Toledo, 1223–1248, Sevilla. A fost etichetat cu numele de „Cel înțelept”, „Astronomul”. El a format un colegiu de 50 de astronomi arabi, evrei și creștini, care în 1252 au scos așa-numitele tabele alfonsinice, efemeridele, dominante până în timpul Renașterii.
154. Ecuații: Ele sunt valabile pentru planetele superioare, iar din punct de vedere geometric semnifică faptul că raza din cadrul epicicloidei, care arată spre planeta respectivă, are mereu direcția Soare-Pământ. Aceasta ca urmare a ipotezei de bază făcută de Ptolemeu, după care perioada de revoluție pe cercul deferent trebuie să fie egală cu perioada siderală, iar cea pe epicicloidă să fie egală cu cea sinodică (Almagest, cartea a 9-a, cap. 6): ambele perioade de revolutie se pot stabili direct din observațiile cerești. Deci avem, scris cu notațiile lui Marte, x₃ = 360°: perioada de revoluție sinodică, x' = 360°: perioada de revoluție siderală, ambele perioade calculate în zile. Dar perioada de revoluție sinodică are de-a face cu Soarele. Ea este perioada în care el o ia înaintea planetei cu exact 360°. x₃ este deci pasul cu care Soarele se depărtează de planetă în medie într-o zi. În mod analog, x' este pasul planetei în raport cu stelele, x₃ + x' deci pasul zilnic al Soarelui față de stele, iar acesta este y. Ecuațiile sunt deci corecte pornind chiar de la noțiunile de perioadă de revoluție siderală și sinodică, înainte să ne referim la cerc deferent și la epicicloidă. Dacă le considerăm acum pe acestea, pornind de exemplu de la o conjuncție, unde Pământul T, Soarele S, centrul C al epicicloidei și planeta P sunt în linie dreaptă, direcția TC se rotește zilnic cu x', CP se rotește cu x₃ și anume conform concepției ptolemeilor – măsurat de la raza TC, în continuare. În timp ce cele două rotații se desfășoară în același sens, CP s-a rotit față de stele cu x₃ + x' = y, deci la fel de mult ca TS, iar TS și CP sunt în permanență paralele. După scurgerea perioadei de revoluție sinodică TS și TP coincid deja conform noțiunii, dar și CP este paralel cu TS și deci C este în linie dreaptă cu T, S și P. Poziția de conjuncție a revenit din nou, prin aceasta confirmându-se potrivirea exactă a ipotezelor ptolemeice. În legătură cu sistemul cosmic ptolemeic, a se compara și cu Astronomie și antroposofie de Elisabeth Vreede, Dornach, 1980, pp. 64–81.
155. sintetizare a pozițiilor determinate empiric ale planetelor: în loc de „îmbinarea pozițiilor din cosmos...”, conform stenogramei.
156. Enigmele filosofiei: vezi nota 67.
157. Dr. Walter Johannes Stein, Viena, 1891–1957, Londra. Inițial matematician, apoi scriitor de orientare filosofică și istorică. Profesor la școala Waldorf.
158. Galilei: vezi Conferința I.
159. Kepler: vezi Conferința I. Expresia acestuia: „Da, eu sunt acela, eu am furat vasele de aur ale egiptenilor pentru a ridica Dumnezeului meu un sanctuar, departe de hotarele Egiptului. Dacă mă iertați am să mă bucur, dacă vă veți supăra am să suport; arunc aici zarul și scriu această carte pentru cititorul de astăzi ca și pentru cel viitor – ce contează?” (Harmonices mundi, 1619, prefață la cartea a 5-a. Traducere de Max Caspar).
160. că în forma cercului se prezintă expresia simplului: „în forma cercului se prezintă” în loc de „cercul reprezintă”, conform stenogramei.
161. Newton: vezi Conferința I .
162. Selenka: vezi Conferința XII-a.
163. Acest lucru este... corect... în privința unui fenomen așa cum este acesta, progresiv: „progresiv” în loc de „programatic”.
164. străbate... organismul cu substanțialități diferite și ceea ce...: „ceea ce” în loc de „că acela”.
165. pe o treaptă anterioară față de cea a animalului: „anterioară” în loc de „superioară”, conform stenogramei.
166. obținem chiar acest punct ideal: vezi Conferința XII-a.
167. cum trebuie să ne reprezentăm procesul: vezi Conferința a VII-a.
168. cu partea opusă polar capului animal: la fel este și în copie și în prima ediție. În stenogramă este scris „capului omenesc” în loc de „capului animal”.
169. Figura 8: răsfrângerea în sus din dreapta este atestată prin dr. H. Poppelbaum, participant la curs.
170. deformare enormă: „enormă” în loc de „metamorfozată”, conform stenogramei.
171. am indicat curba lui Cassini: Conferința a IX-a.
172. în cazul ecuațiilor cu variabilă dublă: vezi Conferința a X-a și Conferința a XI-a.
173. puneți funcții: „funcții” în loc de „ecuații”, conform Conferința a XI-a, unde în acest context înseamnă „... a căror funcționalitate în sine reprezintă o funcție”.
174. antispațiu: prin anii '30 George Adams (-Kaufmann) și, independent de el, Louis Locher-Ernst au început să introducă lumea de reprezentări a geometriei proiective în interpretarea diferitelor indicații date de Rudolf Steiner. (În primul rând a unui pasaj dintr-un răspuns de mai târziu la o întrebare din 12 aprilie 1922, Haga, tipărit în „Die Bedeutung der Antroposophie im Geistesleben der Gegenwart”, Dornach, 1957. O bibliografie completă se găsește la Olive Whicher, în Projective Geometrie, 1970, Stuttgart, cap. IX.)
     Legea dualitării face ca fiecărei structuri formate din puncte să-i corespundă o alta formată din plane; de exemplu, punctelor unei drepte le corespund plane care trec printr-o dreaptă, punctelor aflate într-un plan le corespund toate planele care trec printr-un punct. Unui cub delimitat de șase plane pătrate îi corespunde un octaedru cu șase vârfuri prin care trec patru muchii, celor opt vârfuri prin care trec trei muchii ale cubului le corespund cele opt suprafețe triunghiulare ale octaedrului. Adams și Locher au dezvoltat în operele lor baza conceptuală a realizării concrete a unei „structuri constând din plane”. De fapt, ideea spațiilor create cu altfel de elemente spațiale decât punctul a fost conturată deja în ultimul secol, însă nu a găsit niciodată un interes serios, pentru ca aceasta să servească la descrierea realității. În aparițiile ulterioare, autori precum Bernhard și Gschwind se referă la aceasta („Mathematisch-Astronomische Blätter – Neue Folge”, nr. 1 și nr. 4). – În lucrarea Forțele universale în mecanică, Adams a extins presupunerea sa pe de o parte în fizica teoretică, pe de altă parte în domeniul geometriei superioare. Gschwind, în „Mathematisch-Astronomische Blätter ”, nr. 6, se referă la aceasta și la afirmațiile de bază ale lui Steiner.
175. am menționat-o deseori în alte conferințe: de exemplu în conferința din 30.12.1917 din ciclul Adevăruri ale misteriilor și impulsuri de Crăciun (GA180).
176. în afara cercului abstract: „în afară” în loc de „în interiorul”, conform stenogramei.
177. o sferă mică: „mică” în loc de „aceeași”, conform stenogramei.
178. centrele de observațe: în stenogramă este scris „arcuri” în loc de „observație”.
179. pentru mișcări planetare: „planetare” în loc de „fantastice”, conform stenogramei.
180. stelele duble... se mișcă una în jurul celeilalte: astfel de stele au fost căutate sistematic și cu mult succes, după ce John Michel a afirmat în 1784 că ar exista mult mai multe stele care apar una lângă cealaltă decât se arată întâmplător. Perechile ar avea deci de-a face una cu alta. S-a văzut că acestea se rotese una în jurul celeilalte. Această rotație se reflectă în spectru datorită efectului Doppler. Astfel de mișcări se pot constata în spectru și acolo unde aparent, prin simpla vizualizare, nu se vede decât o stea. Avem în acest caz o „stea spectroscopic-dublă”.
     
     principiului Doppler: se referă la toate procesele ondulatorii. Pentru observatorul care se apropie de punctul de origine al undei, frecvența sa pare mare, iar atunci când se depărtează, pare micșorată. Fenomenul este întâlnit zilnic la șuieratul unui vehicul care trece pe lângă noi. În sensul teoriei ondulatorii a luminii, trebuie să ne așteptăm ca liniile spectrale ale unei stele să fie deplasate spre albastru atunci când steaua se apropie de Pământ și spre roșu atunci când se îndepărtează. W. Huggins a observat în 1867 astfel de deplasări și le-a explicat, conform principiului Doppler, printr-o apropiere, respectiv îndepărtare.
     
     Christian Doppler, Salzburg, 1803–1853, Veneția. Fizician.
181. Când am făcut critica noțiunii de muncă: de exemplu, conferința din 11.8.1919 din ciclul Problema educației ca problemă socială (GA 296).
182. ca în conferințele antroposofice generale să se accentueze mereu: de exemplu, conferința din 25.6.1918 din ciclul Necesități în privința conștienței pentru prezent și viitor (GA 181).
183. mișcarea prin voință se află în: „se află” este adăugat.
184. sub raport psihologic: „psihologic” conform copiei și primei ediții. În stenogramă este trecut „fiziologic”.
185. în institutul nostru de cercetare: acesta a fost înființat în 1920 în Stuttgart cu o secție de fizică și una de biologie, împreună cu asociația economică „Der kommende Tag”, și a ajuns într-o situație proastă pe vremea inflației din anii '20. Mai târziu a putut continua, dar într-un cadru mai restrâns, la Goetheanum-Dornach.
186. în cursul despre căldură: vezi nota 110.
187. în afara nucleului solar: „nucleului solar” în loc de „corpului solar”, conform stenogramei.
188. să aprofundeze lucrurile: observăm, când citim, că între aceste cuvinte și cele care urmează există o pauză. Pasajul care lipsește se referă la un detaliu asupra căruia a avut loc o discuție în cadrul conferinței. Fie că el a părut a se îndepărta de la problema principală, fie că copia a fost considerată aici prea incompletă și întunecată, el a fost omis la prima ediție și trecut la subsol. Cu toate acestea puținele cuvinte au un substrat matematic precis și concludent și aruncă o lumină nouă asupra lemniscatei, atât de importantă pentru întregul curs. Aici trebuie să ne reprezentăm faptul că cuvintele care urmează sunt un răspuns la o întrebare ridicată în cadrul conferinței.
     
     „Ieri, după conferință, unul dintre stimații auditori a făcut o remarcă foarte importantă, importantă din cauză că probabil chiar s-ar fi putut crede că ea a avut o anume influență asupra aspectului principal care a fost examinat aici. Nu este cazul acesta, ci este altceva, și anume: domnul de ieri m-a făcut atent că dacă facem calcule cu ajutorul ecuației curbei lui Cassini va reieși cum ar trebui să trasăm de fapt așa-numita lemniscată. Dacă folosim coordonate polare pentru această curbă, în coordonate obișnuite determinările fiind greoaie, și facem calculele observăm, n-am putut decât să-i dau dreptate domnului după ce am refăcut calculul, că această lemniscată, despre care am vorbit și care este un caz special al curbei lui Cassini – deci dacă trasez aici această formă aparte a curbei lui Cassini (fig. la) – nu am voie să o desenez ca pe un opt, figura 1a, ci ca în figura 1b. Așa reiese în realitate din ecuație. Însă aceasta nu are în principiu nici o influență asupra lucrurilor pe care le-am discutat aici, deoarece chestiunea se schimbă îndată ce vă imaginați că eu nu trasez această lemniscată așa cum am trasat-o în figura 1b ci, în timp ce desenez lemniscata, rotesc planul de desenare în jurul axei lemniscatei, astfel obținându-se de fapt figura 1a.”
     
     
     
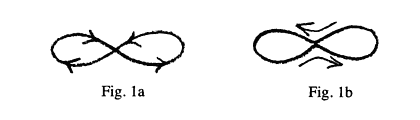
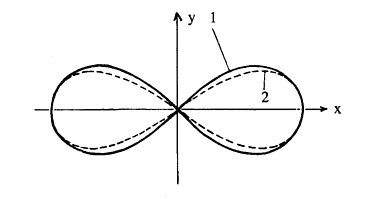
     1 – lemniscata obișnuită
     2 – proiecția lemniscatei de rotație
     
     Abia acum cuvintele care urmează primesc adevăratul lor sens. Dar cum să înțelegem lucrurile mai exact? S-a spus că problema s-ar limpezi doar în coordonate polare. În aceste coordonate, dacă luăm ca unitate de măsură pentru toate lungimile raza vectoare cea mai lungă a lemniscatei, ecuația ei se scrie astfel: r = (cos 2φ)^1/2. În acest caz, dacă cos 2φ devine negativ, r devine imaginar, deci iese din spațiu. Schimbarea semnului are loc când se atinge bisectoarea celor patru cadrane. r este real în ambele sectoare unghiulare tăiate în două de axa x și imaginar în sectoarele traversate de axa y. Întrucât r real este întotdeauna pozitiv, punctele curbei corespunzătoare unghiurilor φ = 45° − α și φ = 135 + α sunt simetrice față de axa y. Între 45° și 135° nu avem nici un fel de punct și la fel între −45° și −135°. La o creștere constantă a lui φ lemniscata evoluează ca în figura 1b, cu un cot brusc. Aproximativ așa trebuie că a fost remarca făcută la conferință. Lemniscata de rotație se simplifică însă cel mai mult dacă rotim planul lemniscatei în jurul celui mai mare diametru al ei cu o viteză egală cu viteza de rotație a razei vectoare în plan. În acest caz unghiul de rotație este tot φ. Proiecția punctului care se mișcă pe planul inițial are același x ca și punctul corespunzător al lemniscatei din planul inițial. y însă este afectat de factorul cos φ. Deoarece pentru punctele reale ale curbei valoarea lui cos φ nu devine niciodată mai mică decât cos 45° = 0,707, proiecția curbei nu se abate niciodată mult față de punctele lemniscatei inițiale. Se abate însă în ceea ce privește modul cum se comportă, deoarece cos φ în al doilea și al treilea cadran este negativ. Dacă lemniscata se parcurge ca în figura 1b proiecția lemniscatei de rotație evoluează după un opt, ca în figura 1a, și viceversa. Dacă unghiul în punctul de întretăiere al lemniscatei este drept, la curba nouă unghiul va fi 2arctg (1:2^1/2) = 70,5°.
189. Cu acest desen în spațiu: „în spațiu” a fost completat.
190. am arătat... avem de-a face cu corpuri de rotație: vezi Conferința a X-a.
191. Aș vrea să indic încă o dată... procesul: indicat în Conferința a XII-a.
192. procesului fizic de plăsmuire a omului: „fizic” este adăugat.
193. această curbă se poate stabili absolut univoc... ca lemniscată de rotație: referirile la mișcarea în formă de lemniscată au preocupat pe mulți comentatori (vezi bibliografia indicată în continuare). Pentru cel avizat, mai facem următoarele remarci:
     
     1. Experimentul și gândirea conceptuală ne învață repede că o buclă plană și în repaus în formă de 8 (lemniscată) nu are o soluție pentru următoarea problemă geometrică: să fie străbătută de două puncte aflate la o distanță aproximativ fixă între ele, astfel încât linia de vizualizare de la un punct spre celălalt să străbată un fascicul de raze plan fără puncte de întoarcere sau opriri. Aceasta este necesară pentru Pământ-Soare.
     
     2. Dacă admitem o mișcare a lemniscatei, suntem într-o foarte delicată situație de a alege, deoarece, dacă ne imaginăm fasciculul de raze mai sus menționat, atunci putem deplasa lemniscata cu două grade de libertate-translație și rotație (spațială) – în jurul dreptei Pământ-Soare.
     
     3. Au fost inițiate studii cu mai mult de o lemniscată, de către L. Locher (1), G. Adams, J. Schultz și alții (2). Mai recent G. Unger și H. Bauer au adus contribuții suplimentare.
     
     4. Literatură bibliografică:
     
     (1) L. Locher-Ernst cu ocazia editării conferinței Omul, o hieroglifă a universului (în ediția Operelor complete sub titlul Corespondențe între microcosmos și macrocosmos GA 201, 1958), în „Mathematisch-Astromischen Blättern”, nr.4 (Dornach, 1942, epuizat; vezi lit. bibl. 3).
     
     (2) Într-un raport al secției de matematică-astronomie de pe lângă Goetheanum din 1967, epuizat de asemenea, s-au făcut diferite încercări, în special cea a lui J. Schultz, având un referat al lui S: Vetter (vezi lit. bibl. 3).
     
     (3) În nr. 121 din „Mathematisch-Physikalischen Korrespondenz” (Dornach 1981) s-au făcut alte referate la lucrările lui Locher și Schultz, s-a prezentat o schiță prealabilă a lui G. Unger cu o lemniscată spațială și s-a reprodus o lucrare detaliată referitoare la o temă a lui H. Bauer.
     
     (4) În biblioteca secției de matematică-astronomie există o culegere bogată a pasajelor corespunzătoare din conferințele lui Rudolf Steiner referitoare la aceasta (cca 100 pagini). Lista cu aceste pasaje poate fi comandată.
194. ecuațiile Bessel: ele se mai numesc și „reducții” sau „corecții” Bessel. Asupra lor Rudolf Steiner a făcut în repetate rânduri trimiteri, atunci când vorbea de mișcarea în formă de lemniscată a Soarelui și Pământul sau de a treia lege de bază a lui Copernic, de exemplu, în afară de aceasta în conferința din 28.09.1919, pomenită în nota 20 și în conferințele Înțelegere socială din punctul de vedere al cunoașterii spiritual-științifice (GA 191, 1972, p. 26). Aceste reducții conțin diferite mișcări și efecte care influențează poziția aparentă a unei stele, pe care Bessel le-a adus la o formă rațional-acceptabilă pentru astronomia practică. Este vorba în general de mărimi mici, prin care însă iese în evidență faptul că în astronomie nu există nimic fix, iar sistemele de coordonate în sine, prin care se face orientarea în spațiu, trebuie și ele înțelese a fi variabile. Cea mai importantă dintre aceste modificări este precesia punctului de echinocțiu de primăvară în valoare de 50,4” anual. Celelalte sunt periodice, cu amplitudinile maxime întâlnite de 20,5” (aberația), 17,2” (nutația pe lungime) și 9,2” (nutația pe înclinația eclipticii) și cu perioadele corespunzătoare de un an, respectiv 18 ⅔ ani și 18 ⅔ ani. Tabele sintetice și modul practic cum se folosesc acestea sunt conținute în anuarele astronomice, cum ar fi Connaissance des Temps, sub titlul de Reducții ale stelelor.
     
     Friedrich Wilhelm Bessel, Minden, 1784–1846, Königsberg. Astronom, la origine negustor.
195. coincide cu Soarele intermediar doar la echinocțiu: „Soarele intermediar” modificat din „Soarele real”. Astfel diferența între timpul real și timpul mediu ar trebui să dispară la echinocțiu. Nu așa se întâmplă, ci în prezent (1979) aceasta are loc la 16 aprilie, 14 iunie, 1 septembrie și 25 decembrie. În cazul confundării „Soarelui intermediar” cu „Soarele real” este vorba evident de o greșeală de scriere sau de vorbire, căci schimbând cuvântul avem exact definiția astronomică a celor trei Sori (a se compara, de exemplu, Rud. Wolf, Manual de astronomie, vol. 2, Zürich, 1892, p. 350 sau P.S. Laplace, Exposition du Système du Monde, ed. a 3-a, Paris, 1808, p. l5). O explicație amănunțită a deosebirii dintre timpul mediu și timpul real se găsește în „Stern-Kalender 1946” al secțiunii de matematică-astronomie de pe lângă Goetheanum.
196. jumătatea lemniscatei... merge în continuare: copia redă aceeași frază cu o altă punctuație: „jumătatea lemniscatei: Pământ, Soare, Pământ, Soare, până ce aceasta a făcut un tur complet; apoi merge în continuare”.
197. figura 6: la prima ediție, figura avea la stânga săgeții mici două semne, întâi un fel de r, apoi un v. Noi credem că r ar fi trebuit înlocuit cu v, lucru care nu s-a făcut.
198. Tycho Brahe: vezi Conferința a II-a.
199. În alte conferințe am menționat... noi ne aflăm în plin conflict: de exemplu, în ciclul de conferințe Puntea între spiritualitatea cosmică și fizicul omului, GA 202, O.C., în special conferința 18.12.1920.
200. Cu alte ocazii am amintit: vezi nota precedentă.
201. spiritualitate a astralului: vezi în Știința ocultă, capitolul „Ființa omului”, compară cu nota 62.
202. o putem urmări... imaginar: cuvântul „imaginar” apare aici rupt de context și rămâne izolat, iar din acest punct de vedere pare a fi o greșeală de stenografiere. În notițele stenografiate pasajul este surprins din păcate doar sumar și nu dă nici o explicație referitoare la problemă. Putem foarte bine însă să credem că „imaginar” a fost pus într-adevăr cu intenție: până acum, în afara observației din Conferința a IX-a, făcută din considerente pur didactice, cuvântul nu a apărut decât în „paranteza” făcută cu puțin înaintea pasajului de față, care prezintă un aspect spiritual-științific cu totul nou; în rest însă imaginarului i se atribuie, într-o formă figurativă, dimensiunea perpendiculară față de cea reală – asemănător cu reprezentarea dată de Gauss. Dacă acum vectorul a–b urmează să dea o componentă oblică, atunci, perpendicular față de direcția acestuia, trebuie să devină activă o altă componentă. În acest sens se poate să fi fost folosit cuvântul. Apariția lui izolată mai trebuie înțeleasă și prin faptul că în conferințe nu intervenea numai ceea ce trebuia spus din capul locului, ci și întrebările care puteau apărea din partea unei anumite persoane-auditor. A se vedea în legătură cu aceasta explicația din „În legatură cu publicarea conferințelor lui Rudolf Steiner”.
203. am menționat deja o comparație: Conferința a X-a.
204. funcții... complicate: „funcții” în loc de „curbe”, conform stenogramei. A se vedea nota 173.
205. Corpul planetar... vi-l puteți reprezenta: „reprezenta” în loc de „înfățișa”, conform stenogramei.
206. ceva ce am prezentat deja metodologic: vezi Conferința a XI-a.
207. În conferințele care se vor ține curând: nu s-au mai ținut.
208. reușita institutului nostru de cercetări fizice: vezi Conferința a XVI-a.
209. am discutat cu un profesor universitar de fizică: nu poate fi vorba decât de Salomon Kalischer (Thorn, 1845–1924, Berlin). Pe vremea aceea, mai multor profesori universitari de fizică nu li s-a publicat Teoria culorilor a lui Goethe, însă Kalischer a reușit aceasta, mai întâi în 1878 în ediția Hempel a operelor lui Goethe apoi și în ediția Sophie 1890–1906. Privitor la corespondența dintre Rudolf Steiner și Kalischer și despre întâlnirea acestora în Arhiva Goethe, a se vedea articolul lui Kurt Franz David din revista „Das Goetheanum”, 1971, p. 281.
210. ne-am explicat puțin... Referitor la Teoria culorilor a lui Goethe: pasajul ar putea suna și în felul următor: „am avut o explicație – el era un newtonian riguros –; în Teoria culorilor la Goethe”, însă nu sunt suficiente puncte de reper în acest sens.
211. să explicăm formarea sistemului ceresc după modelul...: al așa-numitei experiențe Plateau, provenind de la Jos. Ant. Plateau (1873). Această experiență, cât și observația corespunzătoare caracteristică, Rudolf Steiner le-a menționat în multe dintre conferințele sale. Faptul că el încheie cursul de față cu această descriere îi dă acesteia o anumită greutate. Ea conține obiecția centrală împotriva ipotezei nebuloasei originare, respectiv că ea păcătuiește – formulat abstract – în ceea ce privește teza primirii impulsului de rotație. Kant s-a sprijinit pe Newton, iar acesta nu a recunoscut că mecanica elaborată de el implică această limită. Abia atunci, pe vremea când a scris Kant, Euler și-a dat seama, printre alții, de această consecință și a exprimat-o sub forma „legii universale a suprafețelor”. Este o imposibilitate ca nebuloasa originară, de la care a pornit Kant, să ajungă să se rotească prin interacțiune mecanică din interior. Conștientizarea acestui lucru s-a făcut însă încet. Astfel se mai observă la du Prel că el atribuie mecanicii lucruri pe care ea nu le poate face. De aceea un cunoscător atât de experimentat al mecanicii precum Laplace își începea considerațiile sale de la nebuloasa originară, care deja se rotea. Dacă chiar a avut loc întâlnirea sa cu Napoleon, așa cum se spune, atunci el a trecut cu vederea un lucru esențial când la întrebarea acestuia referitoare la rolul lui Dumnezeu în întregul sistem a răspuns: Sire, eu nu am avut nevoie de această ipoteză. – Laplace, conștient sau inconștient, îl pusese pe „domnul profesor” din experiența lui Plateau să învârtă anticipat în vas. A se compara, de asemenea, și Conferința a X-a și nota corespunzătoare.
212. data viitoare vom vorbi iarăși..., dar pornind de la alte puncte de vedere: nu s-a mai ajuns să se facă acest lucru, cel puțin nu în același cerc de oameni. Este posibil ca „celelalte puncte de vedere” să fi fost abordate în ciclul de conferințe, parțial publice, Momentul nașterii științelor naturii în istoria universală și dezvoltarea lor de atunci încoace (GA 326), ținut doi ani mai târziu la Dornach.

AcasăLucrări OnlineIndex GA323Precedenta