Spațiul nostru obișnuit are trei dimensiuni ‒ lungime, lățime și adâncime. O linie are numai o dimensiune, lungimea. Această tablă este un plan, adică, are două dimensiuni, lungime și lățime. Un obiect solid se întinde în trei dimensiuni. Cum apare o figură tridimensională?
Imaginați-vă o formațiune fără nicio dimensiune, și anume punctul. El are zero dimensiuni. Când un punct se mișcă într-o direcție constantă rezultă o linie dreaptă sau o formațiune unidimensională. Acum imaginați-vă dreapta mișcându-se. Rezultatul este un plan care are lungime și lățime. Și, în sfârșit, un plan care se mișcă descrie o figură tridimensională. Nu putem continua însă acest proces pentru a obține prin mișcare dintr-un obiect tridimensional o formațiune cvadridimensională sau o a patra dimensiune. Cum putem folosi imaginile pentru a dezvolta un concept despre a patra dimensiune? Unii matematicieni și oameni de știință ‒ Zollner, spre exemplu ‒ s-au simțit tentați să aducă lumea spirituală în armonie cu lumea noastră senzorială prin presupunerea că lumea spirituală există în spațiul cvadridimensional [Nota 60].
Imaginați-vă un cerc, o figură complet închisă aflată într-un plan. Să presupunem că cineva ne cere să mișcăm o monedă din afara cercului înăuntrul lui (figura 46). Trebuie sau să intersectăm circumferința cercului sau ‒ dacă nu vrem să atingem circumferința ‒ să ridicăm moneda în spațiu și să o așezam înăuntrul cercului, ceea ce cere să părăsim a doua dimensiune și să intrăm în cea de a treia. Pentru a mișca magic moneda înăuntrul unui cub sau a unei sfere trebuie să părăsim a treia dimensiune și să trecem prin cea de a patra dimensiune [Nota 61]. Am reușit să înțeleg în această viață natura spațiului când am început să studiez geometria modernă proiectivă sintetică și să sesizez semnificația transformării cercului în linie dreaptă (figura 47). Lumea este revelată în cele mai subtile gânduri ale sufletului [Nota 62].
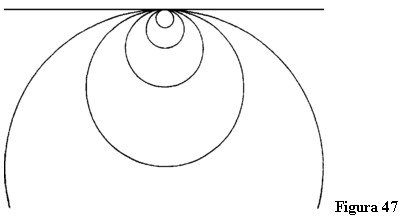
Și acum să ne imaginărn un cerc. Putem trasa circumferința sa și să ne întoarcem la punctul de unde am plecat. Să ne imaginăm cercul crescând tot mai mare, în timp ce linia tangentă rămâne constantă. De vreme ce cercul devine tot mai plat, în cele din urmă va deveni o linie dreaptă. Când trasez aceste cercuri succesiv mai mari, merg întotdeauna în jos pe o parte și vin înapoi în sus de cealaltă parte înainte de a mă întoarce la punctul de plecare. În cele din urmă mă mișc într-o direcție ‒ să spunem spre dreapta ‒ până când ating infinitul. Astfel trebuie să mă întorc din infinit de cealaltă parte, din stânga, de vreme ce succesiunea de puncte dintr-o linia dreaptă se comportă ca un cere. Vedem astfel că spațiul nu are capăt, așa cum o linie dreaptă nu are sfârșit, înșiruirea punctelor sale fiind aceeași ca la cerc. În mod corespunzător, trebuie să ne imaginăm extinderea infinită a spațiului ca fiind conținut în sine, așa cum suprafața unei sfere este închisă în sine. Am descris spațiul infinit cu ajutorul cercurilor și sferelor. Acest concept ne va conduce la conceperea realității spațiului [Nota 63].
În loc să ne imaginăm pe noi înșine îndreptându-ne spre infinit și întorcându-ne neschimbați din cealaltă direcție, haideți să ne imaginăm că purtăm o lumină. Așa cum este văzută dintr-un punct fix de pe dreaptă, lumina radiantă devine din ce în ce mai slabă pe măsură ce ne îndepărtăm cu lumină și tot mai puternică când ne întoarcem cu ea din infinit. Dacă ne imaginăm schimbările în intensitate ca pozitive și negative, avem pozitivul într-o parte și negativul în cealaltă parte. Găsim acești doi poli care sunt pur și simplu efecte opuse ale spațiului în toate efectele din lumea naturală. Acest gând conduce la conceptul spațiului ca fiind ceva plin de forță și la ideea că forțele active în spațiu nu sunt nimic altceva decât manifestări ale acestei forțe însăși. Nu ne vom mai îndoi de posibilitatea de a descoperi o forță care lucrează în interiorul spațiului tridimensional și ne vom da seama că toate fenomenele spațiale sunt bazate pe relații reale în spațiu.
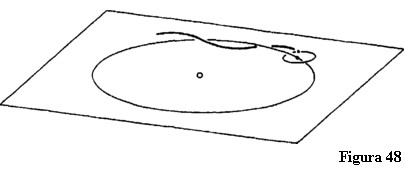
O astfel de relație este împletirea a două dimensiuni. Pentru a face două inele să se întrepătrundă trebuie să-l deschidem pe unul din ele pentru a-l insera pe celălalt. Mă voi convinge acum de varietatea inerentă a spațiului răsucind o bucată dreptunghiulară de hârtie de două ori, adică țin fix un capăt în timp ce răsucesc celălalt capăt cu 360°. Fixez apoi cele două capete ale panglicii cu ace de gămălie. Tăind de-a lungul prin mijloc acest inel răsucit rezultă două inele întrepătrunse care nu pot fi separate fără să-l rupem pe unul din ele. Răsucind pur și simplu panglica am făcut posibilă realizarea în cuprinsul celor trei dimensiuni a unei operațiuni care altfel poate fi efectuată numai prin ieșirea în a patra dimensiune [Nota 64]. Acesta nu este doar un joc; este realitate cosmică. Avem Soarele, orbita Pământului în jurul Soarelui și orbita Lunii în jurul Pământului (figura 48). Pentru că Pământul se mișcă în jurul Soarelui, orbita Lunii și cea a Pământului sunt întrepătrunse așa cum sunt cele două inele de hârtie. În cursul evoluției Pământului, Luna s-a rupt de Pământ. Această separație a avut loc în același fel ca și întrepătrundera inelelor noastre de hârtie. Când privim spațiul în acest fel el devine viu în sine.
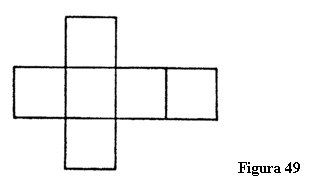
Mai departe să luăm în considerare un pătrat. Imaginați-l mișcându-se prin spațiu până când formează un cub. Mișcarea pătratului trebuie să fie perpendiculară pe poziția sa inițială. Un cub constă din șase pătrate care-i formează suprafața. Pentru a vă da o imagine de ansamblu a cubului pot să așez cele șase pătrate unul lângă celălat într-un plan (figura 49). Pot reconstrui cubul ridicând aceste pătrate în sus, mișcându-le în cea de a treia dimensiune. Al șaselea pătrat este așezat sus. Pentru a forma această figură în cruce am desfăcut cubul în două dimensiuni. Desfășurarea unei figuri tridimensionale o transformă într-o figură bidimensională.
După cum vedeți, frontierele unui cub sunt pătrate. Un cub tridimensional este întotdeauna mărginit de pătrate bidimensionale. Să ne uităm la un singur pătrat. El este bidimensional și este mărginit de segmente de dreaptă unidunensionale. Pot așeza aceste patru segmente într-o singură dimensiune (figura 50). Laturile care definesc una din dimensiunile pătratului sunt desenate în roșu cu linii continue iar cealaltă dimensiune este colorată cu albastru și desenată cu linii punctate. În loc să zic lungime și lățime pot vorbi despre dimensiunile roșie și albastră.

Pot reconstrui cubul din șase pătrate. Asta înseamnă că mă duc dincolo de numărul patru (numărul laturilor pătratului), spre numărul șase (numărul planelor care formează fețele cubului). Făcând un pas mai departe, mergem de la șase la opt (numărul cuburilor care formează „fețele” unei figuri cvadridimensionale). Am aranjat aceste opt cuburi pentru a forma corespunzătorul tridimensional al figurii anterioare, care constă din șase pătrate, în planul bidimensional (figura 51).
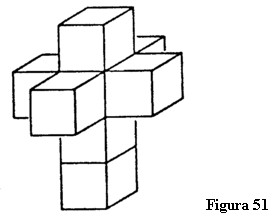
Acum imaginați-vă că aș fi în stare să restrâng această formațiune în așa fel încât să o răsucesc în mod corect și s-o asamblez astfel încât cel de al optulea cub să acopere întreaga formațiune. Folosesc cele opt cuburi pentru a crea o figură cvadridimensională în spațiul cvadridimensional. Hinton numește această figură tessarakt. Frontierele sale constau din opt cuburi, așa cum frontierele cubului constau din șase pătrate. Astfel, un tessarukt cvadridimensional este mărginit de opt cuburi tridimensionale.
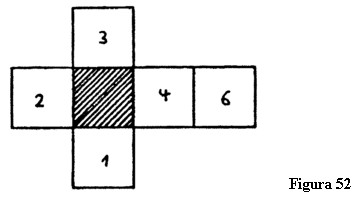
Să ne imaginăm o ființă care poate vedea numai în două dimensiuni. Când privește la pătratele desfășurate ale cubului vede numai pătratele 1, 2, 3, 4 și 6, dar niciodată pătratul 5, cel hașurat din centrul figurii (figura 52). Ceva similar vi se întâmplă când priviți obiectul cvadridimensional desfășurat. Deoarece puteți vedea numai obiecte tridimensionale, nu veți putea vedea cubul ascuns din mijloc.
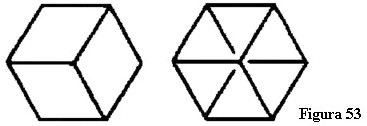
Imaginați-vă acum cubul desenat în așa fel încât conturul său să apară ca un hexagon. Restul este ascuns în spate. Ceea ce vedeți este o imagine-umbră, o proiecție a cubului tridimensional în spațiul bidimensional (figura 53). Imaginea-umbră bidimensională a cubului tridimensional constă din romburi, paralelograme echilaterale. Dacă vă imaginați cubul făcut din fire, puteți vedea și romburile din spate. Această proiecție arată șase romburi suprapuse. În acest fel puteți proiecta întregul cub în spațiul bidimensional.
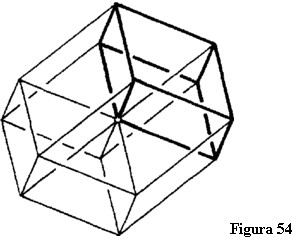
Acum imaginați-vă tessarakt-ul nostru format în spațiul cvadridimensional. Proiectând această figură în spațiul tridimensional trebuie să obținem patru cuburi deformate oblic (paralelipipede) Care nu se întrepătrund: Unul din aceste cuburi deformate oblic ar trebui să fie desenat ca în figura 54.
Opt asemenea cuburi deformate oblic ar trebui însă să se interpenetreze pentru a obține o imagine tridimensională completă a tessarakt-ului cvadridimensional în spațiul tridimensional. Putem descrie prin aceasta umbra tridimensională completă a unui tessarakt cu ajutorul a opt cuburi rombice potrivite care se interpenetrează. Figura spațială care rezultă este un dodecaedru rombic cu patru diagonale spațiale (figura 55). Așa cum în proiecția rombică a unui cub trei romburi adiacente coincid cu celelalte trei în așa fel încât sunt vizibile numai trei din cele șase fețe ale cubului, la fel și în proiecția tessarakt-ului, a dodecaedrului rombic, numai patru cuburi rombice care nu sunt interpenetrate sunt vizibile ca proiecții ale celor opt cuburi-frontieră ale tessarakt-ului de vreme ce patru cuburi rombice învecinate le acoperă complet pe celelalte patru [Nota 65].
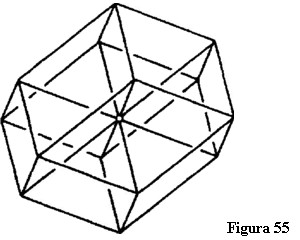
Astfel, putem construi umbra tridimensională a unui corp cvadrimensional, chiar dacă nu tessarakt-ul. La fel suntem și noi înșine umbre ale unor ființe cvadridimensionale. Când trecem de la planul fizic la cel astral trebuie să ne dezvoltăm capacitatea de a forma reprezentări. Imaginați-vă o ființă bidimensională străduindu-se în mod repetat să-și reprezinte în rnod viu o asemenea imagine-umbră tridimensională. Dacă veți construi mental relația dintre dimensiunea a treia și a patra, aceasta va alimenta forțe interioare care vă vor permite să priviți în spațiul cvadrirnensional real, nu matematic.
Vom rămâne întotdeauna neputincioși în lumile superioare dacă nu dezvoltăm facultăți care să ne permită să vedem în lumile superioare aici, în lumea conștienței obișnuite. Ochii pe care îi folosim pentru a vedea în lumea fizică perceptibilă prin simțuri se dezvoltă când suntem încă în pântec. La fel, trebuie să dezvoltăm organe suprasenzoriale când suntem încă în pântecul Pământului, în așa fel încât să putem fi născuți în lumile superioare ca văzători. Dezvoltarea ochilor fizici când ne aflăm în pântecul mamei este un exemplu care luminează acest proces.
Un cub trebuie să fie construit folosind dimensiunile lungimii, lățimii și înălțimii. Un tessarakt trebuie să fie construit folosind aceleași dimensiuni, cu adăugarea unei a patra. Deoarece crește, o plantă iese afară din spațiul tridimensional. Orice ființă care trăiește în timp se eliberează de cele trei dimensiuni obișnuite. Timpul este a patra dimensiune. El rămâne invizibil în cele trei dimensiuni ale spațiului obișnuit și poate fi perceput numai cu puteri clarvăzătoare. Un punct în mișcare creează o linie, o linie în mișcare creează un plan, iar un plan în mișcare creează o figură tridimensiouală. Când se mișcă spațiul tridimensional, rezultatul este creșterea și dezvoltarea. Avem deci, aici, spațiul cvadridimensional, sau timpul, proiectat în spațiul tridimensional ca mișcare, creștere și dezvoltare.
Veți găsi că gândurile noastre geometrice cu ajutorul cărora am construit cele trei dimensiuni obișnuite continuă în viața reală. Timpul este perpendicular pe cele trei dimensiuni și constituie a patra dimensitme. El crește. Când timpul este vitalizat într-o ființă apar abilitățile senzoriale. Când timpul este multiplicat în interiorul unei ființe în așa fel încât are loc mișcarea de sine, rezultatul este ființa animală sensibilă. În realitate, o asemenea ființă are cinci dimensiuni, în timp ce o ființă umană are șase.
Avem patru dimensiuni în domeniul eteric (planul astral), cinci dimensiuni în domeniul astral (Devachanul inferior) și șase dimensiuni în Devachanul superior. Astfel izvorăsc în dumneavoastră variatele manifestări ale spiritului. Când Devachanul își proiectează umbra sa în spațiul astral rezultatul este corpul nostru astral. Lumea astrală aruncată ca umbră în spațiul eteric ne conferă corpul nostru eteric și așa mai departe [Nota 66].
Lumea naturală moare când timpul se mișcă într-o direcție și este revitalizată când se mișcă în cealaltă direcție. Cele două puncte unde se întâlnesc aceste curente sunt nașterea și moartea. Viitorul se îndreaptă continuu spre noi pentru a ne întâlni. Dacă viața s-ar mișca numai într-o direcție nimic nou nu ar apărea vreodată. Ființele umane posedă de asemenea geniu ‒ adică viitorul lor, intuițiile lor care curg spre ele. Trecutul care a fost prelucrat este curentul care vine din cealaltă parte; el determină ființa așa cum a evoluat ea până în momentul prezent.