Subiectul de astăzi ne va confrunta cu unele dificultăți și această conferință ținută la cerera dumneavoastră trebuie s-o considerați ca fiind un episod dintr-o serie. Dacă se urmărește o înțelegere profundă a subiectului, chiar și la un nivel formal, sunt necesare unele cunoștințe matematice. Dar cuprinderea subiectului în toată realitatea sa cere o pătrundere adâncă în esoterism. Astăzi vom fi în stare să ne referim la acest aspect în mod foarte superficial, oferind doar un stimul pentru unii dintre dumneavoastră.
Este foarte dificil să vorbim despre dimensiuni superioare deoarece pentru a ne forma prin reprezentare o părere despre ceva mai mult decât cele trei dimensiuni obișnuite trebuie să intrăm în domenii abstracte, iar aici trebuie să cuprindem conceptele noastre în mod foarte precis și strict, altfel ajungem la ceva fără fundament. Aceasta a fost soarta multor oameni pe care îi cunoaștem, atât prieteni cât și inamici.
Conceptul spațiului multidimensional nu este atât de străin matematicienilor pe cât se crede în general [Nota 67]. Matematicienii fac deja calcule implicând operații pluridimensionale. Desigur, matematicienii pot vorbi despre spații pluridimensionale numai într-o măsură foarte limitată; în mod esențial ei pot discuta numai despre posibilitatea existenței lor. A determina dacă asemenea spațiu este real sau nu trebuie lăsat în seama celor care pot privi în el. Aici avem de-a face numai cu concepte pure care dacă sunt precis înțelese vor clarifica într-adevăr conceptul nostru de spațiu.
Ce este spațiul? În mod obișnuit noi spunem că spațiul este în jurul nostru, că noi umblăm prin spațiu și așa mai departe. Cel care vrea să aibă o reprezentare mai clară despre spațiu trebuie să pătrundă anumite abstracțiuni. Noi numim spațiul în care ne mișcăm tridimensional. Se extinde în sus și în jos, spre dreapta și spre stânga, în față și în spate. Când ne uităm la obiecte le vedem extinzându-se în spațiul tridimensional, adică posedând o anumită lungime, lățime și înălțime.
Trebuie însă să ne ocupăm de detaliile conceptului de spațiu, dacă dorim să dobândim un concept mai precis. Să ne uităm la cea mai simplă formă solidă, cubul. El ne arată în modul cel mai clar ce este lungimea, lățimea și înălțimea. Lungimea și lațimea feței de bază a cubului sunt egale. Când ridicăm această suprafață până când înălțimea sa deasupra poziției inițiale este aceeași cu lungimea și lățimea, obținem un cub, adică o figură tridimensională. Cu ajutorul cubului ne putem informa în modul cel mai clar cu privire la detaliile unei formațiuni tridimensionale. Când examinăm frontierele unui cub găsim că ele constau în suprafețe plane legate prin laturi de lungimi egale. Un cub are șase asemenea suprafețe plane.
Ce este o suprafață plană? În acest punct, cei incapabili de abstracțiuni extreme vor începe să se poticnească. De exemplu, este imposibil să separăm prin tăiere una din fețele unui cub de ceară sub forma unui strat foarte subțire de ceară, pentru că am obține întotdeauna un strat cu o anumită grosime ‒ adică un obiect solid. Nu putem ajunge la granița cubului în acest fel. Frontiera sa reală are numai lungime și lățime, dar nu are grosime. Astfel ajungem la propoziția formală: o suprafață plană este frontiera unei figuri tridimensionale căreia îi lipsește o dimensiune.
Care este atunci frontiera unei suprafețe plane cum este un pătrat? Din nou, definiția cere cel mai înalt grad de abstractizare. Frontiera unei figuri plane este o linie care are doar o dimensiune, lungimea. Lățimea a fost eliminată. Care este limita unui segment de dreaptă? Este un punct care nu are nicio dimensiune. Astfel noi eliminăm întotdeauna o dimensiune pentru a găsi limita unei formațiuni geometrice.
Să urmăm șirul gândurilor a numeroși matematicieni, inclusiv Riemann, care a făcut în acest domeniu o muncă excepțională [Nota 68]. Să considerăm un punct, care nu are nicio dimensiune; o linie, care are una; un plan, care are două; și un obiect solid, care are trei. La un nivel pur tehnic, matematicienii se întreabă dacă este posibil să mai adăugăm o a patra dimensiune. Dacă ar fi așa, limita unei figuri cvadridimensionale ar trebui să fie o figură tridimensională, așa cum un plan este limita unui corp solid, o linie limita unui plan și un punct limita unei linii. Desigur, matematicienii pot trece la considerarea formațiunilor cu cinci, șase, șapte sau chiar n dimensiuni, unde n este un număr întreg pozitiv.
În acest punct apare o anumită neclaritate atunci când spunem că un punct nu are nicio dimensiune, o linie una și un plan două, iar un obiect solid trei. Putem face obiecte solide, cum sunt cuburile, din orice material ‒ ceară, argint, aur și așa mai departe. Materialele sunt diferite, dar dacă le facem de aceeași mărime fiecare ocupă același volum în spațiu. Dacă eliminăm apoi toate aceste materii pe care le conțin aceste cuburi rămânem doar cu anumite segmente specifice din spațiu, imaginile spațiale ale cubului. Aceste segmente de spațiu sunt de aceeași dimensiune pentru toate cuburile, indiferent de materialul din care sunt făcute, și au toate lungime, lățime și înălțime. Putem imagina asemenea spații cubice extinzându-se spre infinit, rezultând astfel spațiul infinit tridimensional. Obiectul material este numai un segment al acestui spațiu.
Următoarea întrebare este dacă putem extinde astfel de evaluări conceptuale, care, plecând de la spațiu, să poată fi extinse la realități superioare? De fapt, matematicianul calculează numai în cazul unor astfel de evaluări; asemenea considerații includ numai numere. Este permis acest lucru? Așa cum vă voi arăta, folosirea numerelor pentru a calcula mărimile spațiului poate da naștere la o mare confuzie. De ce? Va fi suficient să vă spun un singur lucru. Imaginați-vă că aveți o figură pătrată. Eu pot întinde această figură plană spre două direcții, până când ajungem la o figură plană care se extinde la infinit între două linii (figura 56).
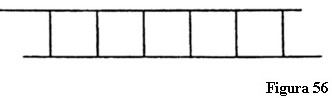
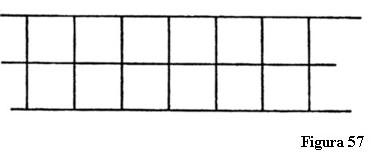
Pentru că această figură plană este extinsă la infinit, mărimea sa este infinită (∞). Acum să presupunem că alți oameni aud că zona cuprinsă între aceste două linii este infinit de mare. În mod firesc, acești oameni se gândesc la infinitate. Dar, dacă le vorbiți de infinitate, ei pot să-și facă, în anumite condiții, reprezentări total greșite despre ceea ce vreți să spuneți. Să presupunem că adaug un pătrat la fiecare din cele existente, adică un al doilea rând de infinit de multe pătrate. Rezultatul este din nou infinitatea, dar o infinitate diferită care este exact de două ori mai mare decât prima (figura 57). Prin urmare, ∞ = 2∞.
În același fel pot să ajung și la ∞ = 3∞. În calculul cu numere, infinitul poate fi folosit la fel de ușor ca orice alt număr finit. Pe cât este de adevărat că în primul caz spațiul este infinit, la fel de adevărat este că ulterior el este 2∞, 3∞ și așa mai departe. Așadar, aici noi lucrăm potrivit numerelor.
Vedeți cum conceptul spațiului infinit legat de o abordare numerică nu ne dă nicio posibilitate de a pătrunde mai adânc în realitățile superioare. Numerele nu au de fapt nicio legătură cu spațiul, ca și boabele de mazăre sau orice alte obiecte. A calcula nu schimbă întru nimic realitatea. Dacă avem trei boabe de mazăre, multiplicarea nu poate schimba acest fapt chiar dacă multiplicăm corect. Calculând că 3x3 = 9 nu vom obține nouă boabe de mazăre. Simpla gândire nu schimbă nimic în asemenea cazuri, iar calculele numerice sunt simplă gândire. Am rămas cu trei boabe de mazăre, și nu cu nouă, chiar dacă am făcut multiplicarea corect. La fel, deși matematicienii fac astfel de calcule referitoare la două, trei, patru sau cinci dimensiuni, spațiul cu care ne confruntăm este numai tridimensional. Sunt sigur că puteți fi ispitiți de asemenea considerații matematice, dar ele dovedesc doar că este posibil să facem calcule privitor la spații cu mai multe dimensiuni. Matematica nu poate dovedi de fapt că spațiul pluridimensional există cu adevărat; nu poate demonstra că acest concept este valid în realitate. Trebuie să fim foarte clari în acest punct.
Să focalizăm acum alte considerente aduse cu deosebită ascuțime de spirit de matematicieni. Noi ființele umane gândim, auzim, simțim în spațiul tridimensional. Să ne imaginăm ființe capabile să perceapă numai în spațiul bidimensional. Astfel de ființe sunt cu totul imaginabile. Organizarea lor corporală le-ar forța să rămână în plan, așa încât ar fi incapabile să părăsească a doua dimensiune. Ar fi capabile să se miște și să perceapă numai spre dreapta și stânga, înainte și înapoi. Nu ar avea nicio idee despre nimic care există deasupra sau sub ele [Nota 69].
Situația noastră în spațiul tridimensional ar putea fi asemănătoare. Organizarea noastră corporală ar putea fi în așa fel adaptată la spațiul tridimensional încât să nu putem percepe a patra dimensiune, ci doar s-o deducem, așa cum ființele bidimensionale ar trebui să deducă existența celei de a treia dimensiuni. Matematicienii spun că este într-adevăr posibil să gândim că ființa umană este limitată în acest fel particular. Desigur, s-ar putea spune și că acesta poate fi pur și simplu un comentariu. Aici este cerută din nou o abordare mult mai exactă, deși chestiunea nu este așa de simplă ca primul exemplu unde am încercat să folosim numere pentru a înțelege infinitatea spațiului. În mod deliberat, mă voi mărgini astăzi numai la explicații simple.
Situația acestei concluzii nu este aceeași ca aceea a evaluării pur formale, a calculului matematic. În acest caz, ajungem într-adevăr la un punct în care putem să ne înșurubăm. Este adevărat că poate exista o ființă care să poată percepe numai ceea ce se mișcă într-un plan. O asemenea ființă ar fi total inconștientă că mai există ceva sus sau jos. Imaginați-vă că un punct din plan devine vizibil pentru ființa respectivă. Desigur, punctul este vizibil numai din cauză că se află în plan. Atât timp cât punctul se mișcă în plan el rămâne vizibil, dar de îndată ce se mișcă în afara planului el devine invizibil. Din punctul de vedere al ființei bidimensionale el dispare. Și acum să presupunem că punctul apare din nou, devine vizibil din nou, dispare din nou și așa mai departe. Când punctul iese în afara planului ființa bidimensională nu-l poate urmări, dar își poate spune: „Între timp punctul a fost undeva unde eu nu îl pot vedea”. Ființa-suprafață ar putea face două lucruri. Haideți să ne furișăm în sufletul acestei ființe bidimensionale. Ea ar putea spune: „Există o a treia dimensiune în care obiectul a dispărut, iar apoi a apărut din nou”. Sau ar putea spune, de asemenea: „Numai proștii pot vorbi despre a treia dimensiune. Obiectul a dispărut pur și simplu și de fiecare dată când a apărut a fost creat din nou”. În ultimul caz ar trebui să spunem că ființa bidimensională păcătuiește împotriva rațiunii. Dacă nu vrea să presupună că obiectul se dezintegrează și este recreat în mod repetat, atunci trebuie să recunoască că obiectul dispare undeva unde ea nu-l poate vedea.
Când o cometă dispare, ea trece prin spațiul cvadridimensional [Nota 70].
Acum vedem ce trebuie adăugat unei abordări matematice a acestei chestiuni. Ar trebui să se găsească ceva în câmpul nostru de observație care apare și dispare în mod repetat. Pentru aceasta nu este necesară clarvederea. Dacă ființa bidimensională ar fi clarvăzătoare ar ști din experiență că există o a treia dimensiune și nu ar trebui să-i deducă existența. Același lucru este adevărat și pentru om. Atât timp cât nu este clarvăzător el este forțat să spună: „Sunt limitat la trei dimensiuni dar de îndată ce observ ceva care dispare și apare periodic sunt îndreptățit să spun că este implicată o a patra dimensiune”.
Tot ce a fost spus până acum este cu desăvârșire incontestabil și confirmarea este atât de simplă încât omului, în starea sa actuală de orbire, nici nu-i va trece prin minte s-o accepte. Răspunsul la întrebarea Există oare ceva care dispare și reapare în mod repetat? este foarte ușor de dat. Gândiți-vă numai la bucuria care răsare uneori în dumneavoastră și apoi dispare. Este imposibil ca cineva care nu este clarvăzător s-o mai poată percepe. Apoi același sentiment reapare din cauza unui eveniment oarecare. Acum, ca ființa bidimensională vă puteți purta în două feluri. Fie vă spuneți că acest sentiment a dispărut într-un spațiu unde nu-l puteți urmări, fie veți fi de părere că sentimentul a dispărut și este creat din nou de fiecare dată când reapare.
Adevărul este că orice gând care dispare în inconștient este dovadă că ceva dispare și apoi reapare. La toate acestea se poate obiecta cel mult ceea ce urmează. Dacă vă străduiți să obiectați împotriva unui astfel de gând plauzibil pentru dumneavoastră, luând în considerare orice obiecție ce ar putea fi adusă de o concepție materialistă, faceți un lucru corect. Voi menționa acum cea mai pertinentă obiecție; toate celelalte sunt foarte ușor de combătut. Oamenii ar putea pretinde că totul se explică în mod pur materialist. Vreau să vă dau un exemplu că ceva poate dispărea și apărea în cadrul proceselor materiale. Imaginați-vă un piston cu aburi în acțiune. Atât timp cât forța acționează asupra pistonului noi percepem mișcarea sa. Acum să presupunem că noi compensăm mișcarea sa cu un piston identic, lucrând în sens opus. Mișcarea se oprește, iar mașina rămâne nemișcată. Mișcarea dispare.
La fel, oamenii ar putea pretinde că senzația plăcerii nu este nimic altceva decât o mișcare a moleculelor în creier. Atât timp cât se mișcă moleculele experimentez plăcerea. Să presupunem că un alt factor cauzează o mișcare opusă a moleculelor. Plăcerea dispare. Cineva care ar putea merge prea departe în evaluările sale ar putea găsi că acesta este într-adevăr un argument important împotriva ideilor prezentate mai înainte. Dar haideți să analizăm mai atent această obiecție. Așadar, după cum mișcarea pistonului dispare ca rezultat al unei mișcări opuse, un sentiment care se bazează pe mișcarea moleculară se spune că poate fi eliminat de o mișcare moleculară opusă. Ce se întâmplă când mișcarea unui piston este compensată de mișcarea celuilalt? Ambele mișcări dispar. A doua mișcare nu o poate elimina pe prima fără a se elimina pe sine. Rezultatul este totala absență a mișcării; nu mai rămâne nicio mișcare. Tot așa niciun sentiment care există în conștiența mea nu ar putea vreodată să elimine altul fără a se elimina totodată pe sine. Presupunerea că un sentiment poate elimina un altul este de aceea total falsă. În caz contrar nu ar mai rămâne niciun sentiment și ar rezulta o totală absență a sentimentului. S-ar mai putea spune cel mult că primul sentiment ar putea fi împins de cel de-al doilea în subconștient. Atunci însă se admite că există ceva care se sustrage observației noastre directe.
Astăzi am vorbit numai despre idei pur matematice fără să luăm în considerare percepția clarvăzătoare. Acum, că am admis posibilitatea să existe o astfel de lume cvadridimensională, ne putem întreba dacă putem observa un obiect cvadridimensional fără a fi clarvăzători. O proiecție de un anume fel ne pemite să facem asta. Putem roti o figură plană până când umbra pe care o aruncă devine o linie. La fel, umbra unei linii poate fi un punct și umbra-imagine a unui obiect tridimensional este o figură bidimensională. Astfel, odată ce suntem convinși de existența unei a patra dimensiuni este firesc să spunem că figurile tridimensionale sunt imaginile-umbră ale figurilor cvadridimensionale.
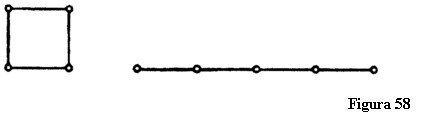
Acesta este un mod pur geometric de a ne imagina un spațiu cvadridimensional. Dar există, de asemenea, un mod diferit de a-l vizualiza cu ajutorul geometriei. Imaginați-vă un pătrat care are două dimensiuni. Acum imaginați-vă cele patru segmente care-l delimitează îndreptate pentru a forma o singură linie. Ați desfășurat formațiunile limită ale figurii bidimensionale în așa fel încât ele sunt așezate într-o dimensiune (figura 58). Să continuăm. Imaginați-vă un segment de dreaptă. Procedăm la fel cum am procedat cu pătratul (înlăturând o dimensiune), în așa fel încât limitele figurii se reduc la două puncte. Astfel, am descris limitele unei figuri unidimensionale în multidimensional. Putem, de asemenea, desfășura un cub așezându-l în șase pătrate (figura 59). Desfacem frontierele unui cub așa încât el este așezat în plan. În acest fel putem spune că o linie poate fi descrisă ca două puncte, un pătrat ca patru segmente iar un cub ca șase pătrate. Observați șirul numerelor: două, patru, șase.
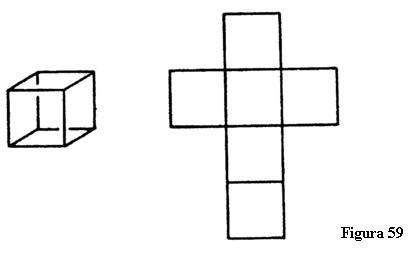
Mai departe luăm opt cuburi. Așa cum exemplele precedente constau din frontierele desfășurate ale figurilor geometrice, cele opt cuburi formează frontierele unei figuri cvadridimensionale (figura 60). Desfășurarea acestor frontiere dă naștere unei cruci duble care reprezintă desfășurarea unui corp cvadridimensional. Hinton numește acest cub cvadridimensional tessarakt.
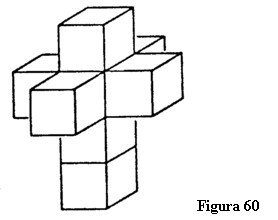
Acest exercițiu ne dă o reprezentare a marginilor unui tessarakt. Ideea noastră despre această figură cvadridimensională este comparabilă cu reprezentarea unui cub pe care ființele bidimensionale ar putea-o avea prin desfășurarea frontierelor unui cub.