| Conferința | Anul | GA | Pagina | Cuvinte cheie |
| 27 noiembrie | 1913 | 324a | Î&R | TR, viteză |
| 1914 | 18 | 590-593 | Einstein, TR, spațiu, timp | |
| 20 august | 1915 | 164 | 251-267 | Viteză, Flammarion (lumen), Einstein, Minkovski, Planck, Poincare |
| 15 aprilie | 1916 | 65 | 657-658 | Conceptul de eter al lui Planck, gravităție |
| 21 august | 1916 | 170 | 178-181 | TR, Einstein, Lorentz |
| 7 august | 1917 | 176 | 239 | TR, Einstein |
| 29 august | 1919 | 294 | 121-123 | Gravitație, TR, Einstein |
| 25 septembrie | 1919 | 300a | 92-93 | TR, Einstein, Lorentz |
| 1 martie | 1920 | 321 | 20-22 | Einstein, TR, refracția și difracția luminii |
| 3 martie | 1920 | 321 | 57 | Einstein, TR, a patra dimensiune |
| 7 martie | 1920 | 324a | Î&R | Viteza luminii, TR, Einstein, (Baravalle) difracția luminii |
| 7 martie | 1920 | 324a | Î&R | Ecuația masă-energie, (Herberg) Einstein |
| 24 martie | 1920 | 73a ediție specială, 1950 |
12-13 | Einstein, Lorentz, masă/energie |
| 27 martie | 1920 | 73a ediție specială, 1950 |
45-51 | TR, eter, viteza luminii, Einstein, Mie, Nordstrom |
| 31 martie | 1920 | 324a | Î&R | Conceptul de eter al lui Planck, TR, materie imponderabilă |
| 18 aprilie | 1920 | 201 | 90-91 | Einstein, TR |
| 24 aprilie | 1920 | 201 | 129-131 | TR, gravitație, Einstein |
| 1 mai |
1920 |
201 | 163 | TR, teoria mercurului! |
| 15 mai | 1920 | 201 | 233 | Einstein, TR, gravitație |
| 22 septembrie | 1920 | 300a | 233 | Einstein (menționat) |
| 15 octombrie | 1920 | 324a | Î&R | TR, viteză, Einstein |
| 15 ianuarie | 1921 | 324a | Î&R | TR, Einstein (menționat) |
| 7 aprilie | 1921 | 76/324a | Î&R | TR, logică (menționată) |
| 12 aprilie | 1921 | 313 | 30 | Eter, Einstein (menționat) |
| 27 iunie | 1921 | 250f | ||
| 28 iunie | 1921 | 205 | 42-13, 51 | Einstein, TR |
| 8 iulie | 1921 | 205 | 150-151 | Einstein, TR, logică |
| 7 august | 1921 | 206 | 110 | Einstein, TR (menționată) |
| 14 octombrie | 1921 | 339 | 74 | Einstein, TR (menționată) |
| 15 octombrie | 1921 | 207 | 168-169 | TR (menționată) |
| 4 noimebrie | 1921 | 208 | 137 | Einstein, TR (menționată) |
| 31 decembrie | 1921 | 209 | 186 | Einstein (menționat) |
| 15 martie | 1922 | 300b | 77 | Einstein (menționat) |
| 12 aprilie | 1922 | 82/324a | Î&R | TR, Einstein, absoluturi |
| 27 decembrie | 1922 | 326 | 68 | TR, Newton (menționat) |
| 2 ianuarie | 1923 | 326 | 113 | TR (menționată) |
| 28 iulie | 1923 | 228 | 25-30 | TR, Einstein, lumină |
| 29 iulie | 1923 | 228 | 52-53 | TR, Einstein, gravitație |
| 29 iulie | 1923 | 291 | 209-210 | TR, Einstein, gravitație |
| 15 septembrie | 1923 | 291 | 126-127 | TR, Einstein |
| 16 noiembrie | 1923 | 319 | Î&R, 141 | TR, proprietăți |
| 2 ianuarie | 1924 | 316 | 25 | TR (menționată) |
| 20 februarie | 1924 | 352 | Î&R, 152 | Einstein, TR |
| 27 februarie | 1924 | 352 | 175-191 | Einstein, TR, Copernic, astronomie |
| 1 martie | 1924 | 235 | 84-85 | TR (menționată) |
| 16 aprilie | 1924 | 309 | 64 | TR, Einstein (menționat) |
| 30 aprilie | 1924 | 300c | 159-160 | TR |
| 17 mai | 1924 | 353 | 248 | TR (menționată), astronomie |
| 20 iulie | 1924 | 310 | 75-76 | TR, Einstein, sunet |
| 22 iulie | 1924 | 310 | 116 | TR (menționată) |
| 19 august | 1924 | 311 | 120-121 | TR, Einstein |
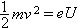 care este atribuită electronilor individuali (cu sarcina electrică e) de
către un câmp electric de voltaj U joacă un rol determinant în toate calculele referitoare la razele catodice. Mai mult, forța K (forța lui Lorentz) cu care este deviată o
sarcină e într-un câmp magnetic B depinde de viteză:
care este atribuită electronilor individuali (cu sarcina electrică e) de
către un câmp electric de voltaj U joacă un rol determinant în toate calculele referitoare la razele catodice. Mai mult, forța K (forța lui Lorentz) cu care este deviată o
sarcină e într-un câmp magnetic B depinde de viteză: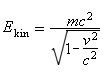
| Conferința | Anul | GA | Conținutul |
| 24 martie | 1905 | 324a | Linia elicoidală |
| 31 martie | 1905 | 324a | Linia elicoidală |
| 1 septembrie | 1906 | 95 | Copernic 3 |
| 16 septembrie | 1907 | 101; 284/285 | Copernic 3 |
| 29 aprilie | 1908 | 98 | Copernic 3, linia elicoidală |
| 7 noiembrie | 1910 | 124 | |
| 21 martie | 1913 | 145 | Circulația sangvină și inima |
| 5 mai | 1914 | 286 | Linia elicoidală |
| 13 iulie | 1915 | 159 | Circulația sangvină și inima |
| 20 august | 1916 | 272 | Copernic 3 |
| 1 octombrie | 1916 | 171 | ∞ |
| 28 mai | 1918 | - | Copernic 3, Bessel |
| 4 septembrie | 1919 | 295 | Copernic 3, Bessel |
| 25 septembrie | 1919 | 300a | Copernic 3, Bessel |
| 26 septembrie | 1919 | 300a | Spirala |
| 28 septembrie | 1919 | 192 | Copernic 3, Bessel |
| 3 octombrie | 1919 | 261 | Copernic 3, Bessel |
| 3 octombrie | 1919 | 191 | Copernic 3, Bessel |
| 10 aprilie | 1920 | 201 | Spirala progresivă |
| 11 aprilie | 1920 | 201 | Circulația sangvină și inima |
| 18 aprilie | 1920 | 201 | ∞, Copernic 3 |
| 1 mai | 1920 | 201 | Bessel, lemniscata progresivă |
| 2 mai | 1920 | 201 | Lemniscata progresivă |
| 15 octombrie | 1920 | 324a | Î&R, Copernic 3, Bessel |
| 2 ianuarie | 1921 | 323 | Copernic 3 |
| 11 ianuarie | 1921 | 323 | ∞, lemniscată |
| 12 ianuarie | 1921 | 323 | ∞, orbite planetare lemniscate |
| 17 ianuarie | 1921 | 323 | lemniscată de rotaxie, Bessel |
| 18 ianuarie | 1921 | 323 | ∞ |
| 26 august | 1921 | 324a | Î&R, Copernic 3 |
| 8 octombrie | 1921 | 343 | Copernic 3 |
| 5 ianuarie | 1923 | 220 | Copernic 3 |
| 5 mai | 1924 | 349 | Copernic 3 |