O întrebare despre necesitatea poziției antroposofice. De ce în problema Einstein trebuie să lucrăm brusc cu semn inversat atunci când trecem de la ponderabil la eter?
Desigur, aceasta se poate face și fără a lua o poziție antroposofică, așa cum se procedează în multe alte domenii științifice pur și simplu prin studierea fenomenelor. Am arătat cum se observă fără prejudecăți fenomenele așa-numitei teorii a căldurii, într-un curs pe care l-am ținut aici pentru o audiență mai restrânsă acum câteva luni [Nota 119]. Trebuie apoi să încercăm să exprimăm aceste fenomene în formule matematice. Particularitatea unor asemenea formule este aceea că ele sunt corecte numai când corespund proceselor pe care le putem observa, adică atunci când rezultatele formulelor corespund și pot fi verificate de realitate. Dacă vreți să înțelegeți ce se întâmplă când un gaz aflat sub presiune este încălzit, veți aplica într-un mod artificial formulele lui Clausius și altele, deși asta se poate face [Nota 120], dar veți constata, așa cum se admite astăzi în mod oficial, că faptele nu corespund formulelor [Nota 121].
În legătură eu teoria lui Einstein găsim în mod ciudat că au fost făcute experimente. Aceste experimente sunt elaborate pentru că se presupune că anumite teorii ar fi corecte. Pentru că experimentele nu au confirmat teoria a fost dezvoltată o altă teorie, bazată exclusiv pe experimente gândite [Nota 122].
Dimpotrivă, dacă încercați să aveți de-a face cu fenomenele căldurii inserând pur și simplu semnele pozitive și negative relevante care depind de tipul căldurii cu care aveți de-a face, conductivă sau radiantă, veți găsi că realitatea confirmă formulele [Nota 123].
Dacă trecem la alte imponderabile, nu este suficient să scriem pur și simplu semnul negativ, ci trebuie să adăugăm și alte relații. Trebuie să ne imaginăm o forță care lucrează radial în domeniul ponderabil. Iar acelea aparținând domeniului eteric ca venind de la periferie, însă cu valori negative, lucrând numai în interiorul unei suprafețe circulare. Astfel, când trecem la alte imponderabile trebuie să inserăm valorile corespondente în mod diferit. Vom descoperi atunci că ajungem la formule care sunt verificate de fenomene.
Aceasta este calea pe care o poate urma oricine, chiar dacă este neimplicat în antroposofie.
Aș dori însă să scot în evidență altceva. Nu trebuie să credeți că ceea ce v-am spus în aceste patru conferințe vi le-am spus așa pentru că eu m-am așezat în poziție antroposofică, ci pentru că ele așa sunt. Și ceea ce este poziție antroposofică urmează numai din faptul că cuprindem cu privirea lucrurile conform cu ele. Atitudinea antroposofică nu precede lucrurile, ci ea rezultă în urma lor. Dacă încercăm să recunoaștem și să înțelegem obiectele și evenimentele fără părtinire, poate urma o atitudine antroposofică. Ar fi rău pentru ceea ce v-am spus dacă ar trebui să plecăm de la o atitudine dictată de prejudecăți. Nu acesta este cazul, ci este o chestiune de a urmări fenomenele într-un mod strict empirie. Atitudinea antroposofică trebuie să fie atunci ultimul lucru; deși nu vreau să susțin nimic altceva decât că ea cu toate acestea poate fi întotdeauna cea mai bună.
După ce a răspuns altor întrebări, Rudolf Steiner spune în concluzie:
Pot doar să subliniez mereu că știința spiritului orientată antroposofic care se dezvoltă aici, la Stuttgart, nu este o mișcare sectantă sau de amatori. Deși forțele sale sunt încă slabe, ea se străduiește pentru a fi o știință reală și autentică. Cu cât va fi testată mai mult știința spiritului cu atât mai mult veți realiza că este adecvată pentru orice metodă de testare științifică.
Multele neînțelegeri care au ca subiect știința spiritului nu sunt rezultatul unui adevărat spirit științific. Oponenții științei spiritului o combat nu pentru că ei înșiși sunt prea științifici, ci pentru că nu sunt științifici îndeajuns, așa cum vor arăta investigațiile următoare [Nota 124]. În viitor însă trebuie nu să slăbim, ci să intensificăm un progres adevărat al aspectului științific; și anume, el nu poate să fie decât un progres de așa natură încât să ne conducă și în domeniul spiritual, nu numai în domeniul material.
ÎNTREBARE: S-a spus că cele trei dimensiuni ale spațiului diferă în structură. În ce constă această diferență?
În orice caz afirmatia nu a fost niciodată formulată astfel: „Cele trei dimensiuni ale spațiului nu sunt la fel în structura lor”, dar aspectul la care probabil vă referiți este următorul. Avem mai întâi spațiul matematic pe care ni-l imaginăm ‒ dacă ne facem o reprezentare exactă a lui ‒ ca fiind format din trei dimensiuni sau direcții perpendiculare pe care le definim printr-un sistem de coordonate de trei axe perpendiculare. Atunci când considerăm acest spațiu din perspectiva uzuală a matematicii noi tratăm cele trei dimensiuni ca și când ele ar fi la fel. Atât de mult nu deosebim dimensiunea sus jos, dreapta-stânga și înainte-înapoi încât chiar credem că pot fi înlocuite una cu alta. În termenii spațiului matematic nu există, la urma urmei, nicio diferență dacă spunem că planul axelor y și x care este perpendicular pe planul format de axele x și z este „orizontal” sau „vertical”. Suntem de asemenea neinteresați de mărginirea acestui tip de spațiu, ceea ce nu înseamnă că în mod obișnuit ni-l imaginăm ca fiind nelimitat. Pur și simplu nu ne interesăm de limitele lui. Presupunem că din orice punct de pe axa x, de exemplu, putem continua să ne mișcăm de-a lungul axei indefinit, fără să atingem undeva capătul.
De-a lungul secolului al XIX-lea metageometria a prezentat multe idei contrare acestei reprezentări a spațiului din geometria euclidiană [Nota 126]. Aș vrea numai să amintesc, de exemplu, cum a făcut Riemann diferența dintre „nemărginirea” spațiului și „infinitatea” spațiului [Nota 127]. Din perspectiva gândirii conceptuale pure nu există, de asemenea, nicio necesitate să presupunem că „nemărginirea” spațiului și „infinitatea” sunt identice. Luați, de exemplu, suprafața exterioară a unei sfere. Când desenați pe o asemenea suprafață nu întâlniți niciodată limite spațiale care v-ar împiedica să continuați să desenați. În cele din urmă, desigur, veți intersecta desenul precedent, dar atâta vreme cât rămâneți pe suprafața sferei nu veți întâlni o limită care să vă forțeze să vă opriți. Astfel, puteți spune că suprafața unei sfere este nemărginită în raport cu capacitatea dumneavoastră de a desena pe ea. Aceasta nu înseamnă că oricine poate pretinde că o asemenea suprafață este infinită. În acest fel, la un nivel pur conceptual, putem distinge nemărginirea de infinitate.
Această distincție se poate extinde și la spațiu, pornind de la anumite premise matematice. Dacă ne reprezentăm că nu vom fi niciodată împiedicâți de a prelungi o axă x sau y prin continuarea adăugării de segmente, această proprietate a spațiului vorbește despre nemărginirea ei și nu despre infinitatea ei. Faptul ca pot continua să adaug mereu segmente nu înseamnă că spațiul este în mod necesar infinit. Poate fi pur și simplu nemărginit. Trebuie să distingem între aceste două concepte. Dacă spațiul este nemărginit dar nu infinit, putem presupune că este în mod inerent curbat și că putem să ne întoarcem într-un anume fel la punctul inițial, ca pe o suprafață sferică. Anumite reprezentări din metageometria modemă depind de asemenea presupuneri. Nu este ușor să se ridice obiecții împotriva acestor presupuneri pentru că nu putem conchide că spațiul este infinit din experiența noastră despre el. Poate fi la fel de bine curbat și finit.
Nu pot duce acest șir de gânduri până la capăt căci el străbate aproape întreaga metageometrie recentă. Găsiți în lucrările lui Riemann, Gauss și ale altora, care sunt ușor de găsit, destule puncte de sprijin pentru a înțelege, dacă sunteți interesați de reprezentări matematice de acest gen [Nota 128]. Acestea sunt argumentele pur matematice împotriva spațiului neutru al geometriei euclidiene. Toate argumentele pe care le-am menționat până acum sunt bazate numai pe conceptul nemărginirii. Întrebarea dumneavoastră este însă înrădăcinată altundeva, în ideea că spațiul pe care-l luăm în calcul, și pe care îl întâlnim în geometria analitică, de exemplu, atunci când avem de-a face cu sistemul de axe coordonate perpendiculare unele pe altele, este o abstracție. Dar ce fel de abstracție? La această întrebare trebuie răspuns mai întâi.
Este vorba dacă trebuie să ne oprim la această abstracțiune „spațiu” sau nu. Este acest spațiu singurul despre care putem discuta? Mai bine spus, dacă acest concept abstract de spațiu este singurul despre care suntem justificați să vorbim, atunci este posibilă o singură obiecție și această obiecție este cea care a fost suficient ridicată în geometria lui Riemann sau în altă metageometrie [Nota 129].
Definițiile lui Kant despre spațiu, de exemplu, se bazează pe un concept foarte abstract despre spațiu. Conceptul său nu se ocupă la început de nemărginire sau de infinitate. În cursul secolului al XIX-lea acest concept a fost zdruncinat de matematică și interior, referitor la conținutul reprezentării sale [Nota 130]. Nici nu poate fi vorba ca definițiile lui Kant să mai poată fi valabile pentru un spațiu care nu este infinit, dar este nemărginit. Mult din ceea ce prezintă Kant mai departe în a sa Critică a rațiunii pure ‒ teoria paralogismelor, de exemplu ‒ ar bate în retragere dacă am fi nevoiți să trecem la conceptul spațiului nemărginit, curbat în sine [Nota 131].
Știu că acest concept al spațiului curb pune probleme modului nostru obișnuit de a ne imagina lucrurile. Dar din perspectivă pur matematic-geometrică, singurul argument posibil împotriva presupunerii că spațiul este curb este acela că ne mișcăm la început într-un domeniu al abstracțiunilor pure care este destul de departe de realitate. Privind situația mai îndeaproape, descoperim că există un curios cerc vicios în deducțiile metageometriei modeme, și anume că ajungem la ele luând ca punct de plecare ideile noastre din geometria euclidiană care nu se preocupă de vreo limitare a spațiului. Trecem apoi la anumite reprezentări derivate ca acelea care se aplică suprafeței sferei. Pe baza acestor deducții și a formelor care rezultă putem să întreprindem anumite transpoziții și apoi să facem reinterpretări ale spațiului. Tot ceea ce se spune presupune geometria euclidiană a coordonatelor. Pe baza acestei presupuneri obținem o anumită curbură. Ajungem la derivații. Toate aceste calcule presupun geometria euclidiană. Aici ajungem la un punct de turnură. Folosim idei ca aceea a curburii pe care le-am dezvoltat numai cu ajutorul geometriei euclidiene pentru a ajunge la o altă reprezentare care poate conduce la un nou punct de vedere și la o nouă interpretare a ceea ce am câștigat din forrnele curbe [Nota 132]. Din punct de vedere fundamental, ne mișcăm într-un domeniu departe de realitate, derivând abstracțiuni din abstracțiuni. Această activitate ar fi justificată numai dacă o realitate empirică ar necesita să ne orientăm cu rezultatele obținute după reprezentările acestora.
Așadar, este vorba de a răspunde la întrebarea: Unde corespunde spațiul abstract experienței noastre? Căci spațiul ca atare, așa cum l-a imaginat Euclid, este o abstracțiune [Nota 133]. În ce constă aspectul său empiric, perceptibil?
Trebuie să luăm ca punct de plecare experiența noastră umană despre spațiu. Ca rezultat al propriei noastre experiențe noi percepem de fapt numai o dimensiune a spațiului, și anume dimensiunea adâncimii. Această percepție elaborată a adâncimii se bazează pe un proces al conștienței noastre adeseori ignorat. Numai că această percepție activă a adâncimii este foarte diferită de reprezentarea unui plan, a unei extensii în două dimensiuni. Când ne uităm afară în lume cu ambii ochi, noi nu știm niciodată că aceste două dimensiuni iau naștere printr-o activitate proprie, printr-o participare a sufletului. Ele sunt acolo ca date, în timp ce a treia dimensiune apare ca rezultat al unei activități care de obicei nu devine conștientă. Trebuie să lucrăm pentru a recunoaște adâncimea, știind cât de depărtat este un obiect față de noi. Noi nu elaborăm extinderea unui plan; ea ne este dată de percepția directă. Folosim însă ambii ochi pentru a prelucra dimensiunea adâncimii. Modul în care experimentăm adâncimea este foarte aproape de granița dintre conștient și inconștient. Dar când învățăm să acordăm atenție unor asemenea procese știm că activitatea niciodată pe deplin conștientă de estimare a adâncimii ‒ este cel mult semiconștientă sau o treime conștientă ‒ este mult mai asemănătoare unei activități raționale, unui proces sufletesc activ, decât orice obiecte privite în plan.
În acest mod noi cucerim activ o dimensiune a spațiului tridimensional în beneficiul conștienței noastre obiective. Și trebuie să spunem că în timp ce privim poziția verticală a omului prin aceasta ne este dat ceva referitor la dimensiunea adâncimii ‒ adică, înainte și înapoi ‒ care o face de neconfundat cu orice altă dimensiune. Faptul că noi experimentăm activ această dimensiune o face să fie de neconfundat cu orice altă dimensiune. Pentru ființa umană dimensiunea adâncimii nu poate fi înlocuită cu nicio altă dimensiune. Este de asemenea adevărat că percepția noastră a bidimensionalității ‒ adică a lui sus și jos, dreapta și stânga, chiar dacă aceste două dimensiuni sunt în fața noastră ‒ este asociată cu părți diferite din creierul nostru, întrucât este inerentă în procesul vederii, deci în procesul senzorial al vederii, în timp ce a treia dimensiune apare pentru noi în acea parte a creierului așezată foarte aproape de centrii asociați cu activitatea rațională. Astfel, vedem că până și în legătură cu viețuirea ei a treia dimensiune prezintă o deosebire esențială față de celelalte două dimensiuni.
Când ne ridicăm apoi la nivelul imaginațiunii părăsim ceea ce viețuim în cea de a treia dimensiune trecând, de fapt, în imaginațiune la reprezentarea bidimensională. La acest nivel mai trebuie să elaborăm și reprezentarea direcției stânga-dreapta, tot așa de ușor de atins ca la elaborarea în domeniul dimensiunii a treia în reprezentarea obiectivă și având și acum o anumită trăire a dimensiunii stânga-dreapta. Apoi, cârd ne ridicăm la nivelul inspirației același lucru este adevărat și pentru dimensiunea sus-jos [Nota 134].
În măsura în care este implicată reprezentarea obișnuită legată de sistemul nostru neurosenzorial, noi ne elaborăm cea de a treia dimensiune. Dar când ne adresăm direct sistemului ritmic, cu deconectarea activității sistemului neurosenzorial, noi viețuim cea de a doua dimensiune. Aceasta are loc într-o anumită măsură când ne ridicăm la nivelul imaginațiunii. Lucrurile nu stau chiar așa, dar ajunge deocamdată. Viețuirea primei dimensiuni o avem când ne ridicăm la nivelul inspirației, adică atunci când înaintăm la al treilea mădular al organizarii noastre umane.
Astfel, ceea ce întâlnim în spațiul abstract se dovedește a fi exact, pentru că toate cuceririle noastre matematice vin dinăuntrul nostru. Consecințele matematice, spațiul tripartit, este ceva ce extragem din noi înșine. Atunci însă când coborâm în noi prin reprezentarea suprasensibilă, rezultatul nu este spațiul abstract cu cele trei dimensiuni diferite având aceeași valoare, ci trei valențe diferite pentru înainte - înapoi, dreapta - stânga, sus - jos. Aceste dimensiuni nu sunt interschimbabile [Nota 135].
Din aceasta mai rezultă și altceva: dacă cele trei dimensiuni nu sunt interschimbabile, nu este necesar nici să ni le reprezentăm cu aceeași intensitate. Aceasta este esențialul spațiului euclidian, că axele x, y și z ‒ se presupune aceasta pentru orice calcul geometric ‒ ni le reprezentăm cu aceeași intensitate.
Dacă vrem să rămânem la ceea ce ne spun ecuațiile geometriei analitice trebuie, dar să acceptăm o intensitate interioară a celor trei axe, atunci ar trebui să ne reprezentăm aceste intensități ca fiind echivalente. Dacă am mări axa x în mod elastic cu o anumită intensitate ar trebui ca și axele y și z să crească cu aceeași intensitate. Cu alte cuvinte, când aplic o anumită intensitate pentru a extinde o dimensiune, forța expansiunii trebuie să fie aceeași pentru toate cele trei axe, adică toate cele trei dimensiuni ale spațiului euclidian. Din această cauză, aș dori să numesc acest tip de spațiu „spațiul rigid”.
Spațiul rigid este o abstractizare a spațiului real care este dezvoltat din ființa umană și principiul echivalenței intensităților nu se aplică la spațiul real. Când considerăm spațiul real nu mai putem spune că intensitatea expansiunii este aceeași pentru toate cele trei dimensiuni. În esență, intensitatea depinde de proporțiile umane care sunt rezultatul intensităților expansiunilor spațiale. De exemplu, luați axa y, direcția sus jos. Trebuie să ne imaginăm intensitatea expansiunii ei ca fiind mai mare decât cea a axei x care corespunde cu direcția stânga-dreapta. Formula care este o expresie abstractă a spațiului real ‒ trebuie să fim conștienți că și această formula este o abstracție ‒ descrie un elipsoid cu trei axe.
Acum ni se oferă prilejul de a ne reprezenta acest spațiu triaxial, în care trebuie să trăiască reprezentarea suprasensibilă, în așa fel în cele trei posibilități de expansiune total diferite, încât cu trăirea celor trei axe reale x, y, z, care ne este dată prin corpul nostru fizic, să recunoaștem acest spațiu ca fiind ceea ce duce concomitent și la exprimarea relației dintre acțiunile corpurilor cerești aflate în acest spațiu. Dacă ne reprezentăm acest lucru, trebuie să considerăm, de asemenea, că tot ceea ce gândim ca existând în universul tridimensional nu poate fi explicat dacă intensitatea expansiunii axelor x, y și z este aceeași, așa cum este cazul cu spațiul euclidian. Trebuie să ne imaginăm că Universul are o configurație care ar trebui reprezentată tot printr-un elipsoid cu trei axe. Mai cu seamă configurația anumitor stele sugerează că această idee este corectă. De exemplu, noi spunem de obicei că galaxia Calea Lactee are forma unei lentile și așa mai departe. Nu putem să ne-o imaginăm ca o sferă. Trebuie să găsim un alt mod de reprezentare, dacă tot rămânem la un fapt pur fizic.
Modul în care este tratat spațiul demonstrează cât de puțin corespunde gândirea modernă cu natura. În timpurile și culturile mai vechi, nimeni nu ajunge la o reprezentare ca cea care a devenit a spațiului rigid, conceptul spațiului fix. Nu putem spune că spațiul euclidian original a încorporat o idee clară a spațiului rigid cu trei intensități de expansiune egale și trei linii perpendiculare. Abia în timpurile recente, când spațiul euclidian a început să fie tratat prin calcule, abstractizarea devenind un atribut esențial al gândirii, a luat naștere reprezentarea abstractă a spațiului [Nota 136]. Cunoștințele pe care le aveau oamenii în Antichitate erau similare cu cele pe care le-am redezvoltat acum pe baza percepției suprasensibile. Puteți vedea din aceasta că lucruri pe care se construiește astăzi foarte mult, fiind considerate de la sine înțelese, au această importanță numai pentru că lucrează într-o sferă care este străină realității. Spațiul cu care suntem obișnuiți astăzi este o abstracțiune. Este foarte departe de orice ne poate învăța experiența. În prezent, suntem adeseori mulțumiți cu abstracțiunile. În vremea noastră, când se pune atât de mult accentul pe empirism, ne raportăm foarte frecvent la abstracțiuni fără ca măcar să fim conștienți de aceasta. Credem că avem de-a face cu lucruri reale în lumea reală. Dar vedeți cât de mult au nevoie ideile noastre de rectificări din acest punct de vedere.
Cercetatorul spiritual nu întreabă pentru fiecare reprezentare dacă este logică. Conceptul de spațiu al lui Riemann este și el cu adevărat logic, deși într-o oarecare măsură este numai o dependință a spațiului euclidian. Nu poate fi gândit însă până la concluziile sale pentru că îl abordăm cu mijloacele unei gândiri foarte abstracte, în timp ce pe baza unei concluzii la care s-a ajuns gândirea este întoarsă cu susul în jos [Nota 137]. Cercetătorul spiritului nu întreabă pur și simplu dacă o idee este logică sau nu. El întreabă dacă ea corespunde sau nu realității. Pentru el acesta este factorul decisiv în acceptarea sau respingerea unei reprezentări. El acceptă o reprezentare când aceasta este conformă cu adevărul.
Corespondența eu realitatea se va folosi ca un criteriu când se va adânci în mod potrivit o reprezentare ca aceea care este o justificare a teoriei relativității. În ea însăși această teorie este cât se poate de logică pentru că este înțeleasă numai în cadrul abstracțiunilor logice. Nimic nu poate fi mai logic decât teoria relativității. Cealaltă întrebare este însă dacă reprezentările ei pot fi realizate. Este suficient să priviți la reprezentările prezentate în aceasta ca fiind analoge și veți descoperi că ele sunt foarte străine de realitate. Ele sunt simple idei aruncate de colo-colo. Ni se spune că aceste idei există numai ca simboluri. Dar ele nu sunt numai simboluri. Fără ele întregul proces ar rămâne agățat în aer [Nota 138].
Aceasta este deci ceea ce am vrut să spun în legătura cu întrebarea dumneavoastră. Așa cum vedeți, nu există un răspuns ușor la întrebări care ating asemenea domenii.
ÎNTREBARE: Să înțelegem că Soarele se mișcă prin spațiu pe o spirală și că Pământul se mișcă de asemenea într-o spirală urmărind Soarele, așadar nu se rotește în jurul Soarelui?
Ar fi realtiv ușor să se discute aceste probleme în detaliu într-o serie mai lungă de conferințe; este însă aproape imposibil să explici ceea ce se află la baza acestui lucru într-un răspuns scurt la întrebare. Voi începe prin a răspunde la întrebările dumneavoastră rezumând pur și simplu rezultatele cercetării de știința spiritului [Nota 140]. Înainte de toate orice concluzie pe care o tragem privitor la relațiile spațiale din Univers, pe baza observațiilor, sunt întotdeauna unilaterale. Sistemul solar ptolemaic a reprezentat o vedere unilaterală și la fel toate celelate modele de sistem solar, inclusiv modelul copernican. Concluziile noastre despre relațiile obiectelor aflate în mișcare, judecate dintr-un anumit punct de vedere, sunt întotdeauna completate sau modificate prin mișcări care nu pot fi apreciate din acest punct de vedere.
După ce am făcut această introducere precaută vă cer să acceptați un alt rezultat al științei spiritului care ne va ajuta să dezvoltăm o concepție despre relația dintre mișcarea Pământului și cea a Soarelui. Trebuie să ne imaginăm că Soarele se mișcă prin spațiu pe un drum curb. Dacă trasăm această curbă destul de departe, se dovedește a fi o formă spirală complicată. O versiune simplificată ar arăta astfel (figura 65a):

Pământul se mișcă de-a lungul aceleiași curbe, urmând Soarele. Dacă luați în considerare diferitele poziții posibile ale Pământului în raport cu Soarele descoperiți că atunci când Pământul este aici un observator ar trebui să privească spre dreapta pentru a a vedea Soarele.
Voi desena acum o altă poziție posibilă (figura 65b).
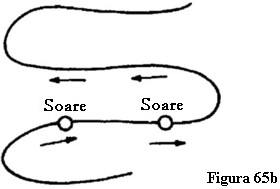
Săgețile indică direcția de privire. Odată privim Soarele dintr-o direcție, iar altă dată din direcția opusă. Dacă vă modelați interior în mod corespunzător acest lucru, veți înțelege ușor că această urmărire a Soarelui de către Pământ se prezintă, în oarecare măsură, prin faptul că alternativ se privește dintr-o parte și din cealaltă, ca și cum Pământul s-ar mișca în jurul Soarelui pe o orbită circulară sau eliptică. În timp ce avem de-a face cu urmărirea Soarelui de către Pământ, această mișcare mai este diferențiată și de anumite relații care ar necesita mai multe ore ca să fie explicate. Adevărul este că numai direcția de privire se rotește.
Așa cum am spus, acest rezumat este rezultatul unor investigații de știința spiritului de lungă durată și se complică și mai mult când luăm în considerare alte relatii. Căci trebuie să ne dăm seama că pe măsură ce obținem o perspectivă mai bună asupra mișcărilor Soarelui sistemul copernican pe care-l prezentăm școlarilor în linii simple devine tot mai complex, până când în cele din urmă liniile nu mai pot fi desenate deloc și oricum ies din domeniul spațial [Nota 141]. Asta este ceea ce am vrut să spun din perspectiva științei spiritului.
Din perspectiva istoriei științelor naturale aș dori să observ că ceea ce uimește în prezent omul la rezultatele cercetării pe care le-am prezentat mai sus există deja în concepția copernicană. Copernic a postulat trei legi. Prima afirmă că Pământul se rotește în jurul propriei sale axe, a doua că Pământul se rotește în jurul Soarelui, iar a treia că mișcarea Pământului în jurul Soarelui oferă numai o explicație provizorie la un nivel conceptual. Ceea ce trebuie admis este faptul că Pământul se află într-o relație cu Soarele [Nota 142].
Această a treia lege dovedește că Copernic era cu adevărat convins că a doua mișcare pe care el o descrie, mișcarea Pămâtului în jurul Soarelui, era numai o convenție făcută pentru ușurința anumitor calcule și că el nu a intenționat să o afirme ca pe un fapt. Astăzi, noi ignorăm în mod consecvent această a treia lege și credem că modelul copernican al sistemului solar cuprinde doar primele două legi. Dacă ar fi să studiem cu adevărat întreaga concepție copernicană am ajunge să acceptăm această concluzie și plecând de la astronomia de calcul, ceea ce ar conduce la acceptarea acestei a treia legi [Nota 143]. Vedeți cum este, de fapt, adeseori, evoluția științifică.
Întrebare despre spațiul pluridimensional.
Putem spune că sistemul axial de coordonate descrie spațiul tridimensional. Acum trecem mai departe pe baza anumitor premise algebrice ‒ discutăm aceasta numai în mod schematic ‒, continuând la un nivel abstract procesul care ne conduce de la un plan la spațiul tridimensional. Ajungem astfel în a patra, a cincea etc. dimensiune, într-un spațiu n-dimensional. Putem chiar construi atunci corpuri cum este tessarakt-ul lui Hinton. Tessarakt-ul nu este însă un corp real, ci doar proiecția adevăratului tessarakt în spațiul tridimensional [Nota 145].
La un nivel pur teoretic și abstract nu există nimic de obiectat unor asemenea deducții. La un nivel teoretic putem de asemenea să trecem de la spațiul tridimensional la cea de a patra dimensiune în timp, folosind formulele și calculele astfel încât să luăm în considerare saltul pe care îl facem, pentru că a trece în timp este diferit de a ne mișca de la prima la a doua, la a treia dimensiune spațială. Rafinând însă acest proces putem într-adevăr face tranziția către timp. Rezultatul este un spațiu abstract cvadridimensional. Dacă rămânem la nivelul pur abstract, ne putem opri în domeniul intelectual atâta vreme cât nu avem nevoie să vizualizăm ceea ce facem. În timp ce șirul nostru abstract de gânduri conduce la un regressus in infinitum, atunci când încercăm să facem asta ne confruntăm intuitiv cu o problemă de elasticitate. Și în cazul pendulului ne putem imagina la început că el va continua să balanseze indefinit, dar în dinamică vom obține o stare oscilatorie. Așa se petrec lucrurile în realitate.
Când ne ridicăm la nivelul percepției imaginative nu putem pur și simplu să repetăm procesul la infint, prin admiterea existenței unei a patra etc. dimensiuni. Dacă folosim notațiile +a pentru prima dimensiune, +b pentru a doua dimensiune și +c pentru a treia dimensiune nu putem, dacă descriem spațiul real, să scriem a patra dimensiune ca fiind +d, ci prin natura lucrurilor suntem forțați să scriem ‒c. A patra dimensiune o anulează pur și simplu pe a treia și rămân doar două. La sfârștiul acestui proces rămânem doar cu două dimensiuni în loc de patru. La fel, dacă presupunem existența unei a cincea dimensiuni trebuie să folosim pentru ea notația ‒b și ‒a pentru a șasea. Adică ne întoarcem la punct [Nota 146]. Prin principiul elasticității ne-am întors la punctul de plecare. Acest fenomen nu este prezent numai în imaginațiune ‒ ca un experiment subiectiv ‒, ci se realizează în felul în care l-am prezentat alaltăieri [Nota 147].
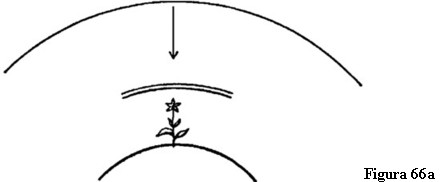
Atâta vreme cât, să spunem, aici avem Pământul și avem în vedere rădăcina plantei (figura 66a), avem de-a face cu o manifestare specifică a gravitației. Aici ne aflăm în cadrul dimensionalității obișnuite a spațiului. Când însă încercăm să explicăm forma florii aceasta nu mai ajunge. Atunci trebuie ca în loc să luăm intersecția axelor ca punct de plecare trebuie să începem cu spațiul infinit care este numai cealaltă formă pentru punct. În loc să ne imșcăm centrifugal înspre în afară trebuie să ne mișcăm centripetal înspre înăuntru (figura 66a). Ajungem la această suprafață ondulată. În loc să se pulverizeze în distanță, se presează din afară, rezultând acele mișcări care sunt mișcări de alunecare sau de răzuire sau mișcări presive, care nu pot fi descrise corect luând intresecția axelor ca punct de plecare al coordonatelor noastre, ci trebuie să luăm ca centru al coordonatelor o sferă infinit de mare și apoi coordonatele îndreptându-se numai spre centru [Nota 148]. Așadar, de îndată ce trecem în domeniul eteric se obține un sistem de coordonate care este, calitativ vorbind, opusul sistemului obișnuit de coordonate. Teoria obișnuită a eterului greșește în a nu lua în considerare această diferență. În aceasta se află cauza pentru care eterul este greu de definit. Este considerat când ca fiind un fluid, când ca fiind un gaz. Greșeala constă în faptul că se pleacă de la sistemul de coordonate privit din punctul central. De îndată ce pătrundem însă în eter trebuie să luăm sfera și să construim întregul sistem din afară spre înăuntru, în loc de a pleca din interior spre afară.

Asemenea chestiuni devin interesante atunci când sunt urmărite matematic trecând în domeniul fizicii. Dacă teoriile noastre care încep să devină aici foarte realiste ar fi duse până la capăt, ar putea contribui la rezolvarea unor probleme de graniță. Numai că, în prezent, asemenea teorii găsesc foarte puțină înțelegere. De exemplu, am încercat o dată să introduc acest subiect într-o conferință la societatea matematică a unei universități [Nota 149]. În acea conferință am arătat că, dacă acestea sunt asimptotele unei hiperbole și acestea sunt ramurile ei, trebuie să ne imaginăm că partea din dreapta se disipează, în timp ce partea din stânga devine convergentă. Adică are loc o inversare completă (figura 66b). Asemenea considerații ne conduc treptat la o tratare mai concretă a spațiului, dar această tratare găsește puțină acceptare. Matematicienii analitici puri sunt deseori într-o oarecare măsură ostili unei geometrii sintetice. Geometria sintetică modernă ne permite să ieșim din matematica pur formală atunci când trebuie înțeles aspectul empiric. Atâta vreme cât aplicăm numai geometria analitică pură nu putem aborda domeniul realității. Geometria analitică ne permite să stabilim numai punctele finale ale coordonatelor, poziția lor geometrică etc. Atunci când limităm construcțiile noastre la linii și cercuri avem nevoie să ne ajutăm de o anumită plasticitate, concretețe. Aceasta face ca geometria analitică să fie atât de benefică în a ieși din formal și de a arăta cum trebuie să concepem elementul matematic în natură [Nota 150].
Întrebare despre teoria relativității
Discuția despre teoria relativității este fără sfârșit [Nota 151]. Cât timp ne plasăm strict pe punctul de vedere al spațiului tridimensional ca spectator al dinamicii Universului, nu poate fi vorba să putem respinge teoria relativității. Atât cât privește percepțiile noastre, desigur, nu există nicio diferență dacă sfera, se aplatizează sau dacă spațiul ca întreg se extinde spre interior în direcția în care se aplatizează sfera. Astfel, atâta vreme cât avem de-a face cu perspectiva spațiului tridimensional, teoria relativității a lui Einstein este absolut corectă. Această teorie a apărut într-un anumit moment în evoluția umanității și a istoriei științei, atunci când am început să gândim în termeni pur spațiali ‒ adică să luăm spațiul euclidian ca punctul nostru de plecare pentru a gândi mai departe și în sensul spațiului neeuclidian ori în sensul teoriei relativității. Este imposibil să se respingă teoria lui Einstein în cadrul spațiului tridimensional.
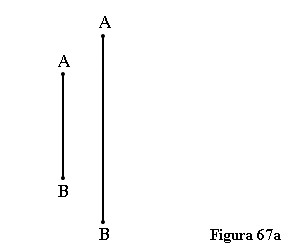
Posibilitatea de a discuta respingerea acestei teorii apare numai atunci când descoperim cum să facem trecerea la domeniul eteric ‒ adică trecerea de la corpul fizic, corpul spațial tridimensional la corpul eteric. Corpul eteric este format în direcție centripetală, nu centrifugală. Și atunci trăiți cu corpul dumneavoastră eteric în interiorul întregului spațiu, a spațiului total. Atunci când de exemplu, observați o distanță între punctul A și punctul B, dacă o aveți ca trăirea dumneavoastră, atunci luați distanța de la A la B ca adevărată o dată ca aceasta și altă dată ca cealaltă (figura 67a). Când conștientizați această situație puteți spune: în momentul în care o am în mine, prima dată sau cealaltă dată unul sau altul dintre puncte trebuie să se fi mutat, în termeni absoluți, dar pentru a face aceasta dumneavoastră înșivă trebuie să stați în totalitatea spațiului. Abia în acest punct discuția devine posibilă. Pentru acest motiv sunt convins că toate discuțiile noastre privind concepte valabile asupra teoriei relativității se vor sfârși cu întrebarea: Păi, de unde știți acest lucru? Dimpotrivă, în momentul în care și trecem la astfel de lucruri, unde ne putem dărui chiar absolutului, adică trecem la vederea interioară, acolo chestiunea începe sa devină în așa fel încât trebuie să spunem: Tocmai în asemenea chestiuni ca teoria relativității se vădește că am ajuns la ceea ce Nietzsche numește punctul de vedere al spectatorului. Acesta în teoria relativității este cultivat până la extrema extremă. Și pentru oricine acceptă acest punct de vedere, teoria relativității este valabilă. Aici nu este nimic de obiectat. În schimb ea poate fi zădărnicită. Un teoretician relativist fanatic din Stuttgart a explicat o dată de ce nu există nicio diferență dacă mergem într-o direcție sau în cea opusă. Dacă țin o cutie de chibrituri într-o mână și un chibrit în cealaltă rezultatul este același, indiferent dacă mișc chibritul pe cutie sau cutia pe chibrit. Desigur, în asemenea cazuri teoria relativității este absolut corectă, dar aș fi vrut să-i strig: Te rog, fă din nou demonstrația după ce fixezi cutia de zid cu un cui!
Aceasta nu diminuează în niciun fel validitatea teoriei relativității. Arată doar că, așa cum putem trece din spațiul bidimensional în dimensiunea adâncimii, putem pătrunde oriunde în lume în elementul spiritual, și atunci încetează teoria relativității să fie adevărată, abia atunci. Acesta este motivul pentru care am spus că discuțiile asupra teoriei relativității tind să meargă la infinit, pentru că strict din punctul punct de vedere al observării ea nu poate fi respinsă. Întotdeauna pot fi aduse contraargumente la contraargumente.
Daca te oprești la pura lume a spectatorului, acolo ca observator stai de fapt întotdeauna în afara a ceea ce observi și trebuie să faci o distincție radicală între subiect și obiect. De îndată ce vă ridicați la niveluri superioare de cunoaștere, această subiectivitate și obiectivitate încetează. Se mai pot spune încă și alte lucruri. Numai că nu este posibil să se spună totul în cadrul unor astfel de răspunsuri la întrebări. Dar aș dori să prezint cel puțin următorul lucru pentru stimulare. Atâta vreme cât rămânem în lumea spectatorului, în lumea spațiului, teoria relativității este ca atare de necombătut. Când ieșim din lumea spectatorului atunci intrăm în lumi unde nu mai suntem doar spectatori, ci unde există participare, de exemplu la durere. Și în clipa când găsiți trecerea de la simpla relație cu alte ființe ‒ și este de înțeles că o teorie a relativității este posibilă numai în cadrul relațiilor ‒, când ajungeți la ceea ce este intrinsec, așadar avansați până la trăirea interioară, în acel moment pentru durere de exemplu, incetează posibilitatea de a specula asupra ei, dacă este relativă sau nu. Din această cauză, nu puteți construi contradicții și apoi să spuneți că deoarece există o contradicție situația nu este reală. În viață, contradicțiile sunt reale pentru că entitățile vieții aparțin unor sfere diferite, care curg una în alta. De îndată ce treceți la realitate nu mai este permis să spuneți: Când stabilesc o contradicție trebuie să o rezolv. Dacă este reală, ea nu poate fi rezolvată. Chestiunea este de fapt, că în lumea relațiilor teoria relativității în mod firesc a trebuit să rezulte. Și dacă ar fi vorba numai de a menține strict punctul de vedere al spectatorului, atunci nu ar fi nimic de obiectat împotriva teoriei relativității. De îndată însă ce intrăm în ceea ce este intrinsec, în durere și bucurie, teoria relativității nu mai stă în picioare.
ÎNTREBARE: Dr. Steiner, ce înțelegeți când spuneți că corpul fizic este un corp spațial în timp ce corpul forțelor formatoare este un corp temporal? Și corpul fizic trăiește în timp atunci când crește și se descompune.
Da, aceasta este doar neprecis gândit, dacă pot să spun așa. Pentru a readuce unei gândiri exacte ar trebui întâi să faceți o analiză a conceptului de timp. Gândiți-vă numai: Așa cum se află în fața noastră realitatea socotită în sensul obișnuit, spațiul și timpul sunt întrețesute. Putem să gândim corpul fizic ca fiind spațial și corpul forțelor formatoare ca fiind temporal numai când separăm spațiul și timpul. În cunoașterea noastră obiectivă obișnuită nu avem de fapt timpul efectiv. Așa cum știți, timpul este măsurat în termenii spațiului; asta înseamnă că schimbările în unitățile spațiale sunt mijloacele prin care cunoaștem ceea ce noi numim timp. Dar acum imaginați-vă un mod diferit de a măsura timpul. Nu mai măsurați timpul în termenii spațiului atunci când treceți la o experiență adevărată a timpului. Aceasta oamenii o fac de cele mai multe ori în mod inconștient. Propriu-zis gândirea noastră este ridicată în conștiență prin cunoaștere imaginativă. Aveți însă o adevărată experiență a timpului, dacă de exemplu, examinați să spunem sufletul vostru la data de 12 aprilie 1922, la 4:04 și eventual tot atâtea secunde.
Vedeți o secțiune temporală a vieții sufletului vostru. Cu toate că nu puteți spune că această secțiune temporală conține vreo secțiune spațială, ea include în primul rând tot trecutul dumneavoastră pământesc și, dacă vreți să-l prezentați schematic, iar curentul experienței dumneavoastră curge de la a la b, trebuie să desenați secțiunea AB (figura 67b).
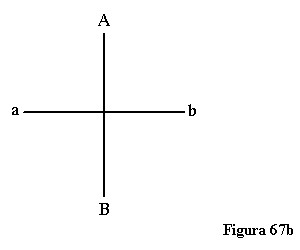
Nu puteți face altceva decât să transpuneți întreaga dumneavoastră experiență în această secțiune, și totuși există în ea o perspectivă. Puteți spune că evenimentele așezate mult în urmă în timp se formează cu mai mică intensitate decât evenimentele mai recente. Totuși, toate aceste evenimente sunt prezente într-o singură secțiune. Astfel încât obțineți alte conexiuni decât cele ce apar când analizați timpul. Putem ridica timpul la nivel de reprezentare numai dacă nu-l analizăm așa cum facem în fizică, conform cu metodele de a înțelege spațiul, ci reflectând doar la viața noastră sufletească. Vă aflați însă în viața dumneavoastră sufletească, chiar și dacă aveți numai gânduri abstracte, în corpul dumneavoastră temporal. Important este să fim în stare să concepem cu adevărat acest corp temporal ca pe un organism. Așa cum știți, atunci când aveți un deranjament digestiv resimțit în stomac, de exemplu, descoperiți că și alte părți ale organismului spațial sunt de asemenea afectate. În organismul spațial, zonele individuale sunt separate spațial una de cealaltă. În organsimul nostru temporal ‒ în ciuda faptului că deosebim între mai târziu și mai devreme ‒, timpii diferiți se află într-o legătură organică. Eu însumi folosesc uneori următorul exemplu. Să admitem că există un om foarte bătrân care, când acesta vorbește cu cei mai tineri, în mod special cu copii, cuvintele lui par că ricoșează; ele nu înseamnă nimic pentru copii. Și găsim alt om care, atunci când vorbește cu copiii, vorbele lui par să curgă direct în sufletele copiilor. Pentru a găsi originea puterii anumitor oameni în vârstă de a binecuvânta pe alții, trebuie să mergeți uneori în copilăria lor timpurie. De obicei nu se studiază probleme ca aceasta pentru că foarte rar este luată în vedere întreaga persoană. Nu este menținută atenția îndeajuns de mult timp pentru a se observa asemenea lucruri. Observația nu se extinde atât de mult. Aceasta trebuie s-o facă antroposofia. Dacă mergeți înapoi, veți găsi că aceia care posedă o putere spirituală neobișnuită de a binecuvânta pe alții la bătrânețe, ale căror cuvinte se revarsă ca o binecuvântare în cei tineri au învățat cum să se roage în propria lor copilărie. Eu exprim acest lucru în imagine astfel: mâinile împreunăte în copilarie devin mâinile binecuvântătoare ale bătrâneții [Nota 152].
Aici vedeți o legătură între influența unei persoane asupra altora la bătrânețe și sentimentul de pioșenie care era prezent în copilăria timpurie a persoanei respective. Calitățile timpurii și târzii sunt legate organic. Există un număr infinit de asemenea conexiuni în fiecare persoană, dar le vedem numai când înțelegem întreaga ființă umană. Astăzi, întreaga noastră viață este exterioară acestei realități. Credem că suntem plini de realitate, dar ne înșelăm pe noi înșine. În cultura noastră de viață de astăzi suntem abstracționiști. Nu acordăm atenție adevăratei realități și de aceea ignorăm calități ca cele pe care le-am menționat. Nu acordăm de asemenea atenție faptului că atunci când prezentăm copiilor ceva, mai ales în clasele elementare, trebuie să evităm să le dăm concepte foarte clar definite. Efectul unor asemenea concepte asupra vieții de mai târziu este similar celui al legării membrelor și a nu le permite acestora să crească. Ceea ce comunicăm copiilor trebuie să fie un organism și trebuie să fie mobil. Astfel ajungem, treptat, la ceea ce numesc eu un organism. Desigur, acest lucru este pe deplin posibil numai în cadrul imaginațiunii. Totuși, ajungem la o reprezentare a unui organism numai dacă realizăm cu claritate că ceea ce în om curge temporal nu se raportează la organismul spațial ci la organismul temporal.
Vedeți acum că timpul posedă o realitate inerentă așa cum o puteți prelua și din matematică. Cred că Oswald ‒ așadar nu un adept al antroposofiei, ci un om care nu este chiar materialist ‒ a fost cel care a indicat într-o frumoasă discuție despre acest subiect că spre deosebire de procesele mecanice procesele organice care au loc în timp nu sunt reversibile [Nota 153]. De fapt, calculele obișnuite rămân întotdeauna exterioare proceselor temporale și nu ne permit să le abordăm. De exemplu, dacă introduceți numere negative în formula de calcul a eclipselor Lunii, obțineți momente dintr-un trecut mai îndepărtat dar nu vă mișcați mai departe cu lucrurile. Vă mișcați numai în sfera spațiului. Astfel dezvoltăm o idee corectă a corpului fizic uman actual numai când suntem în stare să separăm elementul temporal de cel spațial. Aceasta este de o importanță fundamentală în legătură cu omul, pentru că nu putem ajunge la nicio înțelegere a acestuia dacă nu știm că în om elementul temporal își desfășoară cursul ca o entitate în sine și că elementul spațial este guvernat de elementul temporal ca de ceva dinamic. La mașini, elementul temporal este numai o funcție a ceea ce este spațial. Aceasta este diferența. La oameni elementul temporal este ceva real, în timp ce în dispozitivele mecanice elementul temporal este numai o funcție a spațiului. În final, la aceasta se ajunge.
ÎNTREBARE: Einstein spune că continuumul spațiu-timp este cvadridimensional. Dacă înțeleg corect ați spus că a patra dimensiune devine bidimensională în timp ce a patra dimensiune este o a treia dimensiune negativă. Ar putea fi acest lucru interpretat în sensul existenței unei legături între lumea imaginativă și continuumul lui Einstein? Conform cu modul de gândire convențional ar trebui să conchid că lumea imaginativă ar fi un plan specific în spațiul tridimensional, care nu trebuie să fie drept și nici să se afle în spațiu, dar ar trebui să fie posibil să-i confirmăm prezența în orice moment. Este probabil că acest lucru nu este gândit antroposofic, dar aș dori să știu ce are de spus antroposofia despre asta.
Cu excepția câtorva observații, cele scrise de cel ce pune întrebarea sunt gândite foarte antroposofic. Aș dori să adaug următoarele: Este absolut corect că atunci când încercăm să trecem de la cele trei dimensiuni la a patra în mod real și nu abstract trebuie să folosim un semn negativ pentru a descrie a patra dimensiune, adică, trecerea la a patra dimensiune desființează pur și simplu pe cea de a treia, așa cum debitul anulează creditul. Nu există altă cale de a ne imagina situația. Dar dacă ne grăbim pur și simplu spre abstract ajungem la regressus in infinitum care înseamnă existența tot mai multor dimensiuni. Dar acesta este un mod abstract de a continua, nu o observare directă a lucrurilor. Atunci când intrăm în lumea imaginativă avem în adevăr de-a face cu o lume plană, dacă vrem să folosm o expresie luată din geometrie. Avem de-a face cu lumea planului timpului. Aceasta are particularitatea că încetează posibilitatea ca ea să mai fie raportată la cea de a treia dimensiune a spațiului. Aceasta este greu de înțeles, dar veți găsi o situație analogă în geometria sintetică. Aceasta este forțată să considere granița tridimensionalității ‒ dacă impunem granițe lumii tridimensionale ‒ ca o suprafață plană și nu ca o suprafață sferică. Adică, geometria sintetică presupune că spațiul tridimensional este mărginit de un plan. Când atingeți limita tridimensionalității găsiți un plan a cărui limită trebuie imaginată ca o linie dreaptă și nu ca un cerc, iar această linie dreaptă are doar un punct limită și nu două [Nota 154]. În acest loc ajungeți la necesitatea de a nu putea acoperi integral percepția cu gândirea dumneavoastră, cu toate că este consecvent să vorbiți despre un plan ca limită a spațiului tridimensional, despre o dreaptă ca limită a unui plan nu despre un cerc și despre un punct infinit depărtat ca limită a unei linii drepte. Acestea sunt reprezentări reale pentru geometria sintetică. Ea trece în ceea ce devine percepție în lumea imaginativă. Numai că atunci când spunem că lumea imaginativă se află într-un plan nu putem raporta acest plan la spațiul tridimensional definindu-i coordonatele, ci el este scos din spațiul tridimensional și este tot atât de bine undeva ca și peste tot. Asta este dificil de imaginat pentru că suntem obișnuiți să ne reprezentăm lucruri în spațiul tridimensional. Dar lumea imaginativă nu se află în spațiul tridimensional. De aceea nici definițiile tridimensionalității nu îi sunt aplicabile. Avem numai un analog pentru lumea imaginativă în artă atunci când practicăm pictura pornind de la culoare. Când facem asta lucrăm pe o suprafață plană, și chiar dacă lucrăm și pe o suprafață curbă, curbura sa nu se datoreaza picturii, ci altor circumstanțe. Noi lucrăm în plan și avem acum nu numai posibilitatea perspectivei grafice ‒ perspectiva a apărut, așa cum poate știți, foarte târziu în pictură, abia acum câteva secole [Nota 155]; este un lucru nou faptul că noi pictăm în perspectivă, care este numai un corelat pentru spațiu ‒ dar noi avem și perspectiva inerentă culorii [Nota 156]. La Dornach s-a pictat după asemenea principii. Din interiorul sentimentului, nu al gândurilor, galbenul pare că se îndreaptă spre noi atât de tare încât începe să devină agresiv. În contrast, atunci când folosim culoarea albastră, culoarea se retrage. Totuși ambele culori sunt așezate pe aceeași suprafață.
Astfel este posibil să exprimăm fenomene tridimensionale chiar dacă este disponibilă doar o extindere bidimensională. Aceasta este ce aș vrea să dau numai pentru ilustrare, pentru că lumea imaginativă este totuși altceva decât lumea picturală.
Deși ideile exprimate în întrebarea dumneavoastră sunt gândite foarte antroposofic, nu putem spune, fără unele precizări, că pur și simplu lumea imaginativă are o legătură cu continuumul lui Einstein. Continuumul lui Einstein este bazat pe abstracțiune, nu pe percepție. A patra dimensiune a sa este construită ca un analog la celelalte trei dimensiuni, ceea ce nu este acceptabil atunci când ne mișcăm de la cunoașterea obiectivă în spațiu către cunoașterea suprasensibilă reală, care se manifestă mai întâi ca imaginațiune și poate fi exprimată în termeni spațiali numai permițându-i celei de a treia dimensiuni să fie anulată de negativul său. Ceea ce voi spune va părea unora foarte îndrăzneț; totuși este experiența mea. În realitate, situația arată astfel. Atunci când funcționați în lumea obiectivă cu un bun-simț sănătos, orientarea dumneavoastră este derivată numai din cele trei dimensiuni ale spațiului. Prima dimensiune este inerentă posturii dumneavoastră verticale, a doua în direcția stânga-dreapta și a treia în focalizarea ochilor. Dumneavoastră nu sălășluiți în aceste trei dimensiuni atunci când vă aflați în lumea imaginativă. Acolo dumneavoastră sălășluiți numai în două dimensiuni. Dacă ar trebui să localizez aceste dimensiuni în spațiu ar trebui să iau o secțiune verticală prin corpul omenesc. În imaginațiune putem vorbi numai despre dimensiunile lui sus-jos și dreapta-stânga. Când vă mișcați în lumea imaginativă acestea sunt singurele dimensiuni pe care le purtați cu dumneavoastră. Pentru acest motiv nu pot să spun că ele se raportează la un sistem de coordonate în spațiu. Nu pot să le definesc în termenii geometriei euclidiene. Pentru percepția noastră ele sunt reale. Nu are sens să vorbim despre cele trei dimensiuni în contextul lumii imaginative. Trebuie să ne dăm seama că avem de-a face cu o experiență a bidimensionalității, o experiența pe care nu o putem avea în lumea obiectivă. Două dimensiuni sunt o realitate în lumea imaginativă și o singură dimensiune este o realitate în lumea inspirației. Toate inspirațiile se mișcă vertical, dacă vrem să le localizăm în spațiu. Intuiția este punctuală dar nu poate fi raportată nici ea la un sistem de coordonate. În aceste domenii superioare nu putem reveni la spațiul euclidian.
Așa cum ați dedus din conferință se poate face o deosebire între spațiul tactil și cel vizual. Tocmai această deosebire ne poate impulsiona să nu trebuiască să rămânem la observarea elementului matematic pe de o parte și a lumii fizice de cealaltă parte. Așa cum ați putut desprinde din conferința mea [Nota 157], rămâne adevărat că matematica este un produs al spiritului uman sau al ființei umane în general. Și pe măsură ce ne mișcăm mai departe în domenii pur matematice ‒ adică în domenii care sunt delimitate în termeni pur matematici ‒ ajungem tot mai puțin să cuprindem realitatea [Nota 158]; din această cauză vedeți dificultatea care apare mereu în timpurile moderne când se încearcă folosirea matematicii pentru a descrie realitatea.
Dumneavoastră vedeți, de exemplu, trecerea de la sfera infinită din geometria proiectivă la plan și abia veți fi în stare să reconciliați această piatră unghiulară a geometriei proiective cu reprezentările noastre obișnuite despre realitate care sunt bazate pe comportamentul empiric față de lumea din jurul nostru [Nota 159]. În consecință, sarcina noastră ‒ și mulți oameni având pregătirea potrivită ar trebui să lucreze intens în acest sens ‒ este să încercăm să folosim ideile matematice pentru a cuprinde realitatea în domenii foarte concrete [Nota 160]. Despre aceasta aș dori să fac unele precizări, să conturez o problemă. Soluția poate reuși numai dacă matematicienii încep în mod real să lucreze asupra ei. Punerea problemei este următoarea.
Încercați să tratați ceea ce am dezvoltat teoretic ca fiind spațiul tactil în așa fel încât să trebuiască să inserăm pentru trăirea terestră a omului întreaga trăire tactilă, inclusiv dimensionalitatea pe care o conține în relațiile gravitaționale. Omul se află în interiorul gravitației, și dumneavoastră primiți din diferitele direcții periferice cu forțe centripetale pe care le puteți identifica în spațiul tactil posibilitatea de a elabora ecuații diferențiale. Acestea trebuie tratate pentru spațiul tactil în același fel în care tratăm ecuațiile pentru mișcările obligatorii din geometria analitică și mecanica analitică [Nota 161]. Devine apoi posibil să integrăm aceste ecuații, ceea ce ne dă integrale specifice, așadar pentru ceea ce viețuim în spațiu tactil, în timp ce diferențialele ne conduc întotdeauna în afara realității.
Integrând aceste diferențiale se ajunge la diagramele despre care v-am vorbit alaltăieri [Nota 162]. Dacă vreți să captați, pentru aceste diagrame, din nou adevărul, trebuie să o faceți așa cum am indicat în acea conferință. Trebuie să vă mișcați cu ecuațiile integrale în domeniul palpării reale. Prin aceasta vă va deveni evident că pentru palpare dimensiunea verticală are o anume diferențiere, așa încât în această ecuație, dacă însemnați variabila cu x, acesta trebuie să fie precedat de un semn, de exemplu, plus. Aceasta face posibil să stabilim integrale pentru trăirea noastră a spațiului tactil. Dați-mi voie să o formulez schematic astfel:
∫f(x)dy
Rezultatul ar fi integrala pentru trăirile spațiului tactil.
Să mergem mai departe și să aplicăm același principiu spațiului vizual. Încă o dată creăm ecuațiile diferențiale, pe care va trebui să le tratăm în același fel în care am tratat ecuațiile pentru mișcările obligatorii din geometria analitică și din mecanica analitică. Vom vedea că atunci când integrăm obținem integrale foarte asemănătoare dar de așa fel încât, dacă am lua în considerare că variabila x a fost pozitivă, trebuie s-o concepem acum ca fiind negativă. Când tratăm apoi integrarea în acest fel obținem un rezultat care conduce la alte integrale:
∫f(x)dy
Dar când le scad pe cele două una din alta, obțin aproximativ zero. Ele se anulează reciproc. Adică atunci când integrez în raport cu spațiul vizual obțin integrale care le anulează pe cele pentru spațiul tactil. Iar integralele pentru spațiul tactil îmi amintesc foarte mult ‒ numai că ele vor fi mai amănunțite ‒ de toate formulele de care am nevoie pentru circumstanțele și relațiile care se referă la geometria analitică și la ceea ce este mecanic în general, numai că în formulele mecanice trebuie inclusă gravitația.
Obțin integrale pentru spațiul vizual care îmi vor apare foarte utilizabile, numai dacă în mod real ceea ce este spațial la vedere, îl consider de la început cum trebuie matematic. Pentru că pornind de la trivial ridicăm construcții despre vedere și nu considerăm că atunci când avem în vedere spațiul vizual trebuie să calculăm cu mișcarea verticală inevitabilă, că vederea este întotdeauna forțată în necesitatea imperioasă opusă gravitației [Nota 163].
Dacă se ia în considerare acest lucru devine posibil, pe de o parte, să raportăm integralele la mecanică, iar pe de altă parte, la optică. În acest fel obținem mecanica, optica etc. în integrale utilizabile care cuprind realitatea. Nu este pe de-a-ntregul adevărat că diferența dintre integrale este zero, ci rezultă o diferențială. Așadar nu ar trebui să scriem zero, ci trebuie să scriem:
| dx = | ∫ + |
‒ |
∫ ‒ |
Dacă îmi creez posibilitatea ca prin căutări repetate de astfel de integrale și diferențiale să obțin ecuații diferențiale corespunzând lui dx, putem vedea, atunci când îl iau pe dx pozitiv aici și negativ acolo, că dx este un număr imaginar în sens matematic.
Dacă însă acum integrez ecuația diferențială care rezultă, voi viețui un rezultat surprinzător. Puteți trăi acest lucru dacă rezolvați problema corect. Și anume, obțineți formulele acustice și, prin aceasta, acustica. Astfel ați captat cu matematica un adevăr interior. Ați învățat că trebuie să scrieți mecanica în jos pe verticală și vederea în sus pe verticală ‒ lumina este egală cu garvitația negativă ‒, în timp ce auzul are loc pe orizontală. Când puneți la punct aceste calcule nu veți observa numai discrepanțe ‒ matematica pe de o parte și fizica de cealaltă parte ‒ ca un rezultat al ecuațiilor lui Lagrange [Nota 164]. Dar veți vedea că se poate desfășura pe această bază, de asemenea, o muncă fertilă în domeniul matematicii și fizicii la fel cu munca la care m-am referit mai devreme în domeniul filogeneticii [Nota 165].
În această direcție ‒ lucrând asupra lor și nu numai prin observații descriptive, ci prin prelucrare ‒ descoperim diferențe între științele naturale moderne și antroposofie. Va trebui să demonstrăm că în domeniul calculelor ne aflăm în realități întru totul concrete.