U. dezvoltă principiile predării muzicii la clasele I și a II-a.
Rudolf Steiner: N-ar trebui să neglijăm a-i face pe copii să audă ceea ce este obiectiv, despărțit de om, instrumentul. Trebuie să avem grijă ca elevul să ajungă cu destul de mult timp înainte de a împlini nouă ani, în a doua jumătate a clasei a II-a, să se apropie de instrumentul solo, astfel încât pianul s-ar alătura mai târziu pentru aceia care intră aici în discuție. Esențialul în acest domeniu este să începem așa cum trebuie.
T. oferă o continuare a calculului dobânzilor, cu trecerea la calculul algebric. Dacă F = capital final, I = capital inițial, D = dobândă, P = procent, T = timp,
| I × P × T | I × P × T | ||
| atunci F = I + D. Deoarece D = |  |
, atunci F = I + |  |
| 100 |
100 |
Rudolf Steiner: În zilele noastre nu se poate plasa niciodată un capital în această formă. Această formă are o valoare reală numai dacă T este egal cu un an sau e mai mic. Căci în realitate sunt date două cazuri: ori se ridică dobânzile anual, și atunci rămâne mereu același capital inițial, ori se lasă dobânzile la capital, și atunci e nevoie de calcularea dobânzii dobânzilor. Dacă-l lăsăm deoparte pe T, adică, dacă socotim pentru un an, este real. E necesar să le dăm copiilor realitatea.
Va fi bine să lucrăm cu rigurozitate, pentru ca trecerea la calculul cu litere să se facă în mod real. Mai întâi vom dezvolta trecerea de la adunare la înmulțire, apoi de la scădere la împărțire.
Rudolf Steiner explică apoi trecerea de la socotitul cu numere la socotitul cu litere, cu ajutorul următorului exemplu: Scriem mai întâi o sumă a unor numere în care termenii sunt toți diferiți între ei:
20 = 7 + 5 + 6 + 2
Se poate și ca unii din termeni să fie egali:
25 = 5 + 5 + 9 + 6
Și se poate ca toți termenii să fie egali între ei
18 = 6 + 6 + 6.
Dacă începem acum, în felul descris ieri, să înlocuim numerele prin litere, eu am o dată suma S1 = a + a + a, aici sunt trei de a, de trei ori a = 3 × a; apoi S2 = a + a + a + a + a, de cinci ori a = 5 × a; apoi S3 = a + a + a + a + a + a + a, de șapte ori a = 7 × a ș.a.m.d.
Fac asta de multe ori, de nouă ori, douăzeci și una de ori, de douăzeci și cinci de ori. O fac de m ori:
Sm = a + a + a + a + a ... de m ori = m × a.
Obținem astfel din numărul nedefinit al termenilor pe unul din factori, în timp ce adunătorul însuși e celălalt factor. În acest fel se poate dezvolta și înțelege cu ușurință din adunare înmulțirea. În acest fel facem trecerea de la numerele concrete la mărimile algebrice, la a × a = a2, la a × a × a = a3.
Tot astfel se poate deduce din scădere împărțirea.
Dacă-l scădem pe b dintr-un număr foarte mare a, obținem restul r1.
r1 = a - b
Dacă-l scădem încă o dată pe b, obținem restul
r2 = a - b - b = a - 2b
Scăzându-l încă o dată pe b, rezultă:
r3 = a - b - b - b = a - 3b ș.a.m.d.
Putem face aceasta până când din numărul a nu mai rămâne nici un rest, o putem face de n ori:
rn = a - b - b - b - b ... de n ori = a - nb.
Dacă nu mai rămâne nici un rest, adică dacă ultimul rest este 0,
0 = a - nb.
Atunci a a fost împărțit exact, pentru că nu rămâne nici un rest, a = nb. L-am scăzut pe b de n ori, l-am împărțit pe a numai în b-uri, a/b = n, acum a a fost consumat în întregime. Am constatat că pot face aceasta de n ori și am trecut astfel de la scădere la împărțire.
Putem spune: Înmulțirea este un caz particular al adunării, împărțirea este un caz particular al scăderii, numai că nu adăugăm, respectiv nu scoatem afară doar o dată, ci de multe ori.
Vine vorba despre numerele negative și imaginare.
Rudolf Steiner: Un număr negativ este un scăzător pentru care nu mai există descăzut; o invitație la o operație pentru care nu mai există substanță, care nu poate fi executată. ‒ Eugen Dühring [Nota 40] a respins numerele imaginare drept absurdități și a spus despre felul cum a definit Gauß numerele imaginare că este o măgărie, că nu ele nu ar fi o realitate, ci o fantasmagorie.
Așadar, dezvoltăm întotdeauna înmulțirea din adunare și pe urmă ridicarea la putere din înmulțire. Apoi, împărțirea din scădere, extragerea rădăcinii din împărțire.
| adunare înmulțire ridicare la putere |
scădere împărțire extragerea rădăcinii |
Abia după ce începem socotitul cu litere, de pe la unsprezece, doisprezece ani, trecem la ridicarea la putere și la extragerea rădăcinii, pentru că la extragerea rădăcinii joacă un rol important ridicarea la putere a unui polinom algebric.
În acest context mai trebuie să se facă următoarele lucruri: calcularea venitului brut, a venitului net, a tarei, a ambalajului.
Se pune o întrebare cu privire la folosirea formulelor.
Rudolf Steiner: Acum se pune problema dacă preferați să nu folosiți prea des formula, ci să parcurgeți tot mereu raționamentul descris ‒ aici putând, în orice caz, să vă ocupați de dezvoltarea vorbirii, e bine să faceți așa ceva -, sau dacă vreți să treceți, totuși, la formulă. Dacă procedați într-un mod plin de tact, în așa fel încât formula să fie înțeleasă bine, și acest lucru este cât se poate de folositor pentru a practica până la un anumit punct dezvoltarea vorbirii.
Dar, începând de la un anumit moment, e bine, de asemenea, să facem în așa fel încât formula să fie ceva față de care copilul să aibă sentimente. Să facem din formulă ceva care are viață interioară, astfel încât, de pildă, dacă la
| C × P × T | |
| D = |  |
| 100 |
T devine mai mare, copilul să aibă sentimentul că totul se mărește.
Cu aceasta a fost spus ceea ce voiam să vă spun referitor la aceste lucruri, și anume că numerele concrete ar trebui folosite cu un asemenea prilej, ca și la calcularea dobânzilor și procentelor, pentru a face trecerea spre socotitul cu litere și pentru a dezvolta în legătură cu aceasta înmulțirea, împărțirea, ridicarea la putere și extragerea rădăcinii. Sunt lucruri care trebuie să fie făcute neapărat cu copiii.
Acum, eu aș vrea să pun întrebarea: Considerați că e bine să-i învățați pe copii ridicarea la putere și extragerea rădăcinii înainte să fi trecut la socotitul cu litere sau ați face acest lucru numai după aceea?
T.: Ridicarea la putere ‒ înainte, extragerea rădăcinii ‒ după aceea.
Rudolf Steiner: Așadar, dvs. porniți, și ar trebui ca și pe viitor să porniți, de la a face cât mai devreme, de pe la unsprezece, doisprezece ani, trecerea la socotitul cu litere, făcând abia după aceea ridicarea la putere, extragerea rădăcinii. Căci, după ce s-a învățat socotitul cu litere, se poate face cu copiii într-un mod foarte simplu și economic ridicarea la puterea a doua, a treia, la alte puteri, și extragerea rădăcinii, pe când înainte s-ar cere teribil de mult timp pentru aceasta. Veți preda ușor și într-un mod economic, dacă ați discutat mai întâi cu copiii socotitul cu litere.
E. prezintă un mod de a trata, pentru elevii ultimei clase, sub raport istoric, întemeierea și dezvoltarea orașelor și vorbește, referindu-se la perioada năvălirilor maghiare, de „Germania”.
Rudolf Steiner: Eu aș fi aici foarte atent ca nu cumva să ia naștere niște reprezentări confuze. Bineînțeles că în acea vreme, în timpul lui Heinrich, supranumit „Constructorul de orașe”, Germania nu exista. Trebuie să ne exprimăm cam așa: orașe de pe Rin sau de pe Dunăre, care mai târziu au devenit germane. Nu-i așa, înainte de secolul al X-lea nici nu avem de-a face cu maghiarii; înainte, în cazul unor asemenea năvăliri, era vorba de huni, de avari. Începând cu secolul al X-lea, putem spune, desigur, „Germania”.
Aici, de pildă ‒ aceasta este o temă care se tratează cu elevii ultimei clase din ciclul elementar ‒, eu aș căuta să dezvolt în copii o idee despre cronologie. Dacă spunem așa, „secolul al IX-lea, secolul al X-lea”, reprezentarea devine prea puțin concretă. Cum ați proceda pentru ca în copii să ia naștere o reprezentare concretă despre timp?
Ați putea să le explicați copiilor: „Dacă tu ai acum vârsta pe care o ai, ce vârstă au mama ta, tatăl tău? Și ce vârstă au bunicul și bunica?” ‒ Scoateți la suprafață întregul șir al generațiilor și-l puteți face pe copil să înțeleagă că un asemenea șir de trei generații constituie aproximativ o sută de ani. Așadar, în o sută de ani trăiesc trei generații. Deci, acum o sută de ani străbunicii erau copii. Acum nouă secole nu au fost trei generații, ci 9 x 3 = 27 generații ‒ „Ia imaginează-ți că tu”, în spunem copilului, „ții mâna tatălui tău, acesta ține mâna bunicului tău, acesta ține mâna străbunicului tău ș.a.m.d. Dacă ar sta așa unul lângă altul, al câtelea bărbat ar fi Heinrich I, al câtelea bărbat li s-ar fi împotrivit maghiarilor în jurul anului 926? Ar fi cel de al douăzeci și șaptelea bărbat.” ‒ Acest lucru l-aș înfățișa în modul cel mai sugestiv. După ce i-am condus pe copii în mod corect la reprezentarea despre ce mult e de atunci, le-aș descrie invaziile maghiarilor. Le-aș spune că în Europa Centrală au năvălit pe atunci maghiarii. Că maghiarii s-a năpustit cu o sălbăticie care a făcut ca toți să fie nevoiți să fugă, până și copiii din leagăne au trebuit să fie duși pe vârfurile munților. Că maghiarii năvălitori au ars până la pământ sate și păduri. Aș descrie în modul cel mai sugestiv invazia maghiară.
E. arată în continuare cum Heinrich, știind că în cetatea fortificată Goslar a putut ține piept maghiarilor, a luat hotărârea de a întemeia orașe fortificate și că în acest fel s-a ajuns la numeroase întemeieri de orașe.
Rudolf Steiner: N-ați putea face încă o dată această prezentare din punctul de vedere al istoriei culturii și civilizației? Căci afirmația că Heinrich ar fi întemeiat aceste orașe este o legendă istorică de o tentă cam monarhistă. Toate aceste orașe din secolul al X-lea existau deja în linii mari, ca târguri. Ele doar au fost stimulate în dezvoltarea lor, prin faptul că oamenii care locuiau în vecinătatea acestor orașe s-au aliat pentru a se putea apăra mai bine de maghiarii năvălitori, făcând astfel mai puternice aceste localități. Aici au acționat niște motive mai mult economice, care au dus la formarea de orașe. Heinrich n-a făcut prea mare lucru în această privință.
V-aș ruga doar să prezentați toate acestea într-un mod foarte sugestiv, să procedați într-un mod cât mai viu, pentru ca în copii să ia naștere imagini lăuntrice sugestive, astfel încât copiii să poată "pipăi" cu adevărat totul. Trebuie să vă puneți în mișcare fantezia și să folosiți lucruri de felul celor pe care vi le-am arătat când a fost vorba să faceți în așa fel încât timpul să devină concret. Nu câștigăm cu adevărat nimic dacă știm în ce an s-a dat, de pildă, lupta de la Zama ș.a.m.d., dar dacă ne reprezentăm, dacă știm: Carol cel Mare se trage dintr-o viță cu treizeci de strămoși, dacă ne-am întinde mâinile de-a lungul generațiilor, am obține prin aceasta o reprezentare sugestivă, concretă despre timp. Atunci, acest timp vine mult mai aproape de noi ‒ da, privește, el vine mult mai aproape! ‒, dacă știm că-l putem găsi pe Carol cel Mare într-o linie genealogică de treizeci de strămoși.
T.: Oare n-ar fi bine ca la asemenea prezentări de istoria culturii și civilizației să se atragă atenția și asupra gândirii și simțirii cu totul diferite ale oamenilor din aceste epoci?
Rudolf Steiner: Da, asupra acestui lucru am atras atenția și cu alte prilejuri în conferințele mele. În primul rând, asupra faptului că e bine să prezentați într-un mod cât mai sugestiv marele avânt din preajma secolului al XV-lea, simțirea și gândirea cu totul diferite ale oamenilor dinainte de această epocă și de după ea. De pildă, deja Lamprecht, pe care însă nu vreau să-l recomand în mod cu totul deosebit, se străduie să constate o cu totul altă gândire și simțire a oamenilor care au trăit înainte de această epocă. ‒ Documentele n-au fost încă deloc cercetate în această privință.
Dacă vreți să vă transpuneți puțin în studiul istoriei culturii, va trebui să puteți dezvolta deja un anumit simț de a percepe asemenea lucruri, iar dacă veți avea un asemenea simț pentru a percepe atât lucrurile mai generoase, cât și lucrurile mai meschine, pe care le povestesc autorii, atât lucrurile cele mai filistine, cât și cele cu orizont mai larg, veți putea ajunge la reprezentări mai juste despre fenomenele istoriei culturii și civilizației.
Rudolf Steiner recomandă, în urma unei întrebări, să se achiziționeze pentru biblioteca dascălilor:
Buckle, “Istoria civilizației din Anglia”;
Lecky [Nota 41], “Istoria iluminismului din Europa”.
Cu ajutorul acestora se poate cultiva metoda pentru studiile de istoria culturii și civilizației. Din Lamprecht ar intra în discuție părțile mai vechi, dar multe lucruri sunt prezentate strâmb și subiectiv.
Dacă nu v-ați însușit acest instinct de a percepe forțele reale care impulsionează istoria culturii, riscați să socotiți, cu o îngustime de minte, cu un diletantism, asemănătoare cu cele ale lui Wildenbruch [Nota 42], că dramele împăraților și regilor și încăierările de familie cum ar fi, de pildă, cea dintre Ludovic Piosul și fiii săi, ar fi niște fenomene esențiale din istoria culturii.
Cartea lui Gustav Freytag [Nota 43] „Imagini din trecutul Germaniei” este foarte bună; totuși, nu avem voie să ne lăsăm molipsiți prea mult de această tihnă a unei istorii scrise pentru mătuși amatoare de cafea. Tocmai în perioada actuală noi trebuie să ieșim din cadrul stilului de gândire și simțire care există în lucrările acestor reprezentanți ai literaturii de pe la mijlocul secolului al XIX-lea, stilul lui Gustav Freytag, Julian Schmidt ș.a.m.d. Lassalle [Nota 44] l-a poreclit „Schmulian Jüd”, la Lassalle această poreclă nu avea o semnificație antisemită.
Se pune o întrebare cu privire la lucrarea lui Houston Stewart Chamberlain, „Temeiurile secolului al XIX-lea”.
Rudolf Steiner: Și în cazul lui Chamberlain [Nota 45] trebuie să dezvoltăm mai întâi simțul potrivit, fiindcă ce scrie el este pe un sfert ceva plin de duh, dar trei sferturi sunt fraze goale, vorbărie nesănătoasă. La el putem citi multe lucruri foarte bune, dar trebuie să dobândim noi înșine o privire de ansamblu și să ne formăm o părere personală. Descrierile istorice sunt mai bune în cărțile lui Buckle și Lecky. Chamberlain este mai mult așa, un purtător de smoking. El este, totuși, un domn cam vanitos, care nu trebuie considerat chiar o autoritate, dar care a făcut unele observații juste. De altfel, sfârșitul său n-a fost prea frumos, mă refer la procesul cu „Frankfruter Zeitung”.
Se amintește de scrierile lui Kautsky [Nota 46].
Rudolf Steiner: Da, dacă iei de regulă contrariul a ceea ce el arată. De la socialiștii moderni primim un material faptic bun și interesant, dacă nu ne lăsăm amăgiți de teoriile care străbat descrierile lor.
O imagine ciudată oferă și Mehring [Nota 47], în felul cum mai întâi îi mustră pe social-democrați în cartea sa, în istoria social-democrației, câtă vreme a fost liber-cugetător; apoi, după ce a trecut la social-democrați, el nu face decât să-și mute critica asupra liber-cugetătorilor.
M. prezintă o introducere în noțiunile fundamentale ale geografiei matematice pentru elevii de treisprezece ani, observații asupra răsăritului de Soare și a orbitei parcurse de Soare.
Rudolf Steiner: După ce i-ați făcut pe copii să iasă sub cerul liber, mai târziu puteți să transformați foarte bine acest lucru în desen și să aveți grijă să existe un anumit paralelism între desen și cele văzute de copii afară. Numai că trebuie să vă sfătuiesc să nu folosiți prea mult dintr-o dată elementul linie. Este foarte important să-i învățăm pe copii aceste lucruri, dar dacă sintetizăm prea mult, îi facem pe copii să nu mai înțeleagă și să nu mai rețină. Putem include elementul linie în orele de geografie și geometrie. Asemenea expuneri s-ar încheia, probabil, cu dezvoltarea noțiunilor de ecliptică și coordonate.
A. dezvoltă aceeași temă, răsăritul și apusul de Soare, pentru copiii mai mici, și caută să explice mersul Soarelui [Nota 48] și al planetelor cu ajutorul unui desen schematic.
Rudolf Steiner: Ei bine, această înțelegere a lucrurilor își va pierde tot mai mult din importanță, pentru că ceea ce s-a presupus de atunci încoace cu privire la aceste mișcări nu este absolut just. În realitate, avem de-a face cu o asemenea mișcare (Rudolf Steiner desenează la tablă):
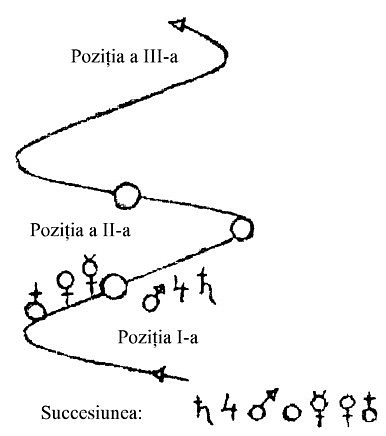
Avem, de pildă, Soarele aici (poziția I) aici sunt Saturn, Jupiter, Marte, iar aici sunt Venus, Mercur, Pământul. Acum, toate se mișcă în direcția indicată (linia elicoidală), una după alta, în așa fel încât atunci când Soarele a trecut dincoace (poziția a II-a), Saturn, Jupiter, Marte, sunt aici, iar Venus, Mercur și Pământul, dincoace. Și acum, Soarele se rotește mai departe și merge într-acolo (poziția a III-a). Prin aceasta, ia naștere iluzia că Pământul se învârte în jurul Soarelui. În realitate, Soarele merge înainte, iar Pământul se târăște în urma lui.
B. prezintă o descriere din cadrul culturii și civilizației Vechiului Egipt.
Rudolf Steiner: Înainte de toate, ar trebui să arătăm ce înseamnă celălalt principiu, cu totul diferit de cel actual, de a reproduce ceva. Vechii egipteni aveau deficiența că nu vedeau în perspectivă. Vechiul egiptean pictează fața din profil, iar restul corpului văzut din față. Ar trebui să-i facem pe copii să cunoască această particularitate a modului de a percepe lumea.
Pe urmă, ar trebui să stabilim legătura dintre desenul pictural al egiptenilor și principiul pe care-l aveau, care ține de istoria naturală, că înfățișau oamenii cu cap de animal și așa mai departe. Deja din vremuri foarte vechi a fost împinsă foarte departe comparația dintre om și animale. Am putea să-l învățăm apoi pe copil ceea ce este prefigurat în orice cap uman, lucru pe care, parțial, copilul îl mai vede și astăzi [Nota 49]. Egiptenii mai percepeau această înrudire dintre fizionomia omului și animale. Ei se mai aflau pe această treaptă de percepție copilărească.
B. întreabă ce ar trebui să li se spună, de fapt, copiilor în legătură cu piramidele, când se discută despre ele.
Rudolf Steiner: Este, firește, extraordinar de important să căutăm treptat să punem și pentru copii ceea ce e just în locul a ceea ce e greșit. De fapt, piramidele erau lăcașuri de inițiere. Și aici ajungem să le transmitem copiilor noțiunea de învățământ superior din Egipt, care era totodată o inițiere. Trebuie să le povestim ceva din cele ce se petreceau acolo. Aici se săvârșeau acțiuni religioase, așa cum sunt săvârșite ele astăzi în biserici, acțiuni care făceau însă, totodată, să poată fi cunoscut Universul. Vechiul egiptean și învăța, atunci când i se arăta, în cadrul unor acțiuni religioase solemne, ceea ce se petrece în Univers și în evoluția omenirii. Serviciul religios și învățământul religios erau una. De fapt, învățământul și actul cultic se confundau.
B. descrie munca de ridicare a piramidelor și obeliscurilor și spune că ar trebui să presupunem că pentru aducerea, prelucrarea și zidirea uriașelor blocuri de piatră, trebuie să fi fost nevoie de mai multe milioane de oameni. El spune că trebuie să ne întrebăm cum de a fost posibil cu mijloacele tehnice din acea vreme să se miște din loc și să se așeze unul peste celălalt uriașele, grelele blocuri de calcar și de granit.
Rudolf Steiner: Da, dar veți face să ia naștere în copii niște reprezentări absolut corecte numai spunându-le că, dacă ar lucra oameni cu forța corporală actuală, ar fi nevoie de două ori și jumătate mai mulți oameni. Dar, în realitate, vechii egipteni aveau de două ori și jumătate mai multă forță corporală decât oamenii din zilele noastre, cel puțin aceia care au lucrat la ridicarea piramidelor și a altor monumente de acest fel. Existau, firește, și oameni mai slabi.
B. întreabă dacă trebuie să intrăm în mitologie.
Rudolf Steiner: Nu-i așa, dacă nu putem înfățișa mitologia egipteană în adevărata ei formă, trebuie să renunțăm la acest lucru. Dar dacă suntem în stare să prezentăm mitologia egipteană în adevărata ei înfățișare, atunci s-o facem. În Școala Waldorf ar fi foarte bine să formăm deja la copii noțiunile juste legate de mitologia egipteană, pe care o putem cunoaște, desigur, foarte bine, dacă vrem să ne adâncim în ea.
K. face o expunere [Nota 50] legată de elaborarea noțiunilor: loc geometric, cerc, elipsă, hiperbolă, lemniscată. (Acest lucru urmează să fie continuat a doua zi.)