Pentru că voi începe prin a discuta aspecte elementare ale celei de a patra dimensiuni, ceea ce veți auzi astăzi vă va putea dezamăgi, dar abordarea lor în detalii de mai mare profunzime ar cere o reală cunoaștere a conceptelor superioare ale matematicii. Aș dori pentru început să vă înzestrez cu concepte foarte generale și elementare. Trebuie să distingem între realitatea spațiului cvadridimensional și posibilitatea de a gândi despre el. Spațiul cvadridimensional are de-a face cu o realitate care depășește cu mult realitatea senzorială obișnuită. Când intrăm în acest domeniu trebuie să ne transforrnăm gândirea și să ne familiarizăm cu modul în care gândesc matematicienii.
Trebuie să ne dăm seama că la fiecare pas pe care îl fac matematicienii trebuie să fie conștienți de efectul pe care acesta îl are asupra întregului curs al raționamentului. Când ne ocupăm de matematică trebuie să realizăm, de asemenea, că înșiși matematicienii nu pot face măcar un singur pas în realitatea celei de a patra dimensiuni. [Ei pot ajunge la concluzii doar plecând de la ceea ce poate fi sau nu gândit.] Subiectele cu care vom avea de-a face sunt la început simple, dar se pot complica atunci când abordăm conceptul celei de a patra dimensiuni. Întâi trebuie să fim lămuriți asupra a ceea ce înțelegem prin dimensiuni. Cea mai bună cale pentru a obține claritate este de a verifica dimensionalitatea diferitelor obiecte geometrice, care apoi ne vor conduce la considerații care au fost făcute prima dată de mari matematicieni ca Bolyai, Gauss și Riemann [Nota 1].
Cel mai simplu obiect geometric este punctul. Nu are absolut nicio extindere; el poate fi numai gândit. El este fixarea unei poziții în spațiu. Nu are nicio dimensiune. Prima dimensiune este dată de o linie. Linia dreaptă are o dimensiune, lungimea. Când mișcăm o linie care nu are grosime, ea părăsește prima dimensiune și devine un plan. Un plan are două dimensiuni, lungime și lățime. Când mișcăm un plan el părăsește aceste două dimensiuni. Rezultatul este un corp solid cu trei dimensiuni, înălțime, lățime și adâncime (figura 1).
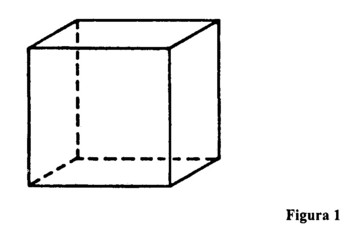
Când mișcați un corp solid (de exemplu, un cub) prin spațiu, rezultatul este tot un corp tridimensional. Nu-l puteți face să părăsească spațiul tridimensional mișcându-l.
Mai există încă câteva concepte de care avem nevoie. Să considerăm un segment de linie dreaptă. Are două limite, două puncte finale, A și B (figura 2).

Să presupunem că vrem să facem ca punctele A și B să se suprapună. Pentru a face asta trebuie să îndoim segmentul. Ce se întâmplă atunci? Este imposibil să facem ca punctele A și B să se suprapună dacă rămânem în dreapta unidimensională. Pentru a uni aceste două puncte trebuie să părăsim linia dreaptă ‒ adică prima dimensiune ‒ și să intrăm în a doua dimensiune, planul. Când facem să-i coincidă capetele, segmentul devine o curbă închisă, de exemplu un cerc (figura 3).
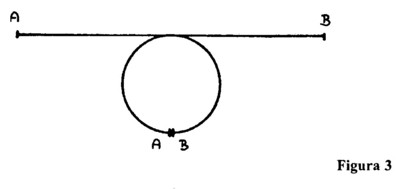
Un segment de linie dreaptă poate fi transformat într-un cerc numai părăsind prima dimensiune. Puteți relua acest proces cu o suprafață dreptunghiulară dar numai dacă nu rămâneți în cele două dimensiuni. Pentru a transforma dreptunghiul într-un cilindru sau tub, trebuie să intrați în a treia dimensiune. Această operație este îndeplinită în același mod ca cea precedentă în care am adus la suprapunere cele două puncte, părăsind prima dimensiune. În cazul unui dreptunghi, care este așezat în plan, trebuie să ne mișcăm în a treia dimensiune pentru a face ca cele două capete să coincidă (figura 4).
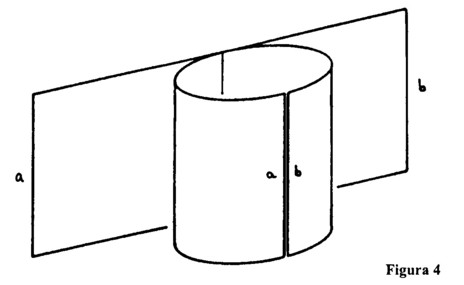
Putem oare imagina o operație asemănătoare cu un obiect care are deja el însuși trei dimensiuni? Gândiți-vă la două cuburi congruente ca limite ale unui corp tridimensional. Puteți face ca unul din cuburi să alunece în celălalt. Acum imaginați-vă că un cub este roșu pe o față și albastru pe fața opusă. Singurul mod de a face acest cub să coincidă cu celălalt, care este geometric identic dar ale cărui fețe roșie și albastră sunt inversate, ar fi să întoarcem unul din cuburi și apoi să-l facem să coincidă cu celălalt (figura 5).
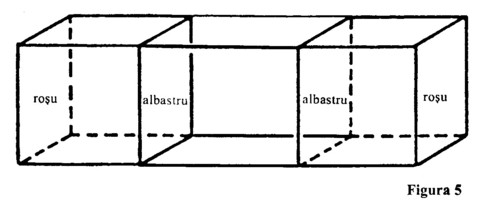
Să considerăm un alt obiect tridimensional. Nu puteți pune mănușa stângă pe mâna dreaptă. Dar dacă vă imaginați o pereche de mănuși care sunt imagini simetrice una alteia în oglindă și apoi luați în considerare segmentul de linie dreaptă cu capetele sale A și B, puteți vedea cum de fapt mănușile aparțin una alteia. Ele formează o singură figură tridimensională cu o suprafață limită (planul oglindă) în mijloc. Același lucru este adevărat pentru cele două jumătăți simetrice ale pielii unei persoane [Nota 2]. Cum pot fi făcute să coincidă două obiecte tridimensionale care sunt simetrice una alteia? Numai părăsind a treia dimensiune așa cum am părăsit prima și a doua dimensiune în exemplele precedente. O mănușă dreaptă sau stângă pot fi trase pe mâna stângă, respectiv dreaptă numai trecându-le prin spațiul cvadridimensional [Nota 3]. În construirea adâncimii, a treia dimensiune a spațiului perceput, noi suprapunem (tragem) imaginea ochiului drept peste cea a ochiului stâng, cu alte cuvinte, contopim cele două imagini [Nota 4].
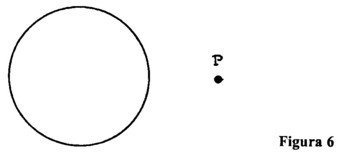
Și acum să considerăm unul din exemplele lui Zollner [Nota 5]. Aici avem un cerc și, în afara lui, un punct P (figura 6). Cum putem aduce punctul P în interiorul cercului fără să tăiem circumferinta? Nu putem face asta dacă rămânem în plan. Așa cum am avut nevoie să părăsim cea de a doua dimensiune și să intrăm în a treia pentru a face tranziția de la pătrat la cub, trebuie de asemenea să părăsim a doua dimensiune în acest exemplu. La fel, în cazul sferei, este imposibil să ajungem în interior fără să străpungem suprafața sferei sau fără să părăsim a treia dimensiune [Nota 6].
Acestea sunt posibilități conceptuale, dar sunt de semnificație practică pentru epistemologie, în mod special cu privire la problema epistemologică a obiectivității conținuturilor percepției. Întâi trebuie să înțelegem clar cum percepem de fapt. Cum dobândim cunoștințe despre obiecte prin simțuri? Vedem o culoare. Fără ochi nu am percepe-o. Fizicienii ne spun că ceea ce se află afară în spațiu nu este culoare, ci doar mișcare spațială care intră în ochi și este preluată apoi de nervul optic și transmisă la creier unde apare, de exemplu, percepția culorii roșii. Mai departe ne putem întreba dacă culoarea roșie există și în cazul în care nu există senzația.
Nu am putea percepe culoarea roșie dacă nu am avea ochi sau sunetul soneriei dacă nu am avea urechi. Toate senzațiile noastre depind de tiparele de mișcare care sunt transformate de aparatul nostru fizico-psihic. Chestiunea devine și mai complicată dacă ne întrebăm unde este localizată acea unică calitate pe care noi o numim roșu. Este pe obiectul pe care îl percepem sau este un proces vibrațional? O mulțime de mișcări care își au originea în afara noastră intră în ochi și se continuă în creier. Oriunde vă uitați găsiți procese vibraționale și procese nervoase, nicidecum culoarea roșie. Nu o veți găsi de asemenea nici studiind ochiul însuși. Ea nu se află nici în afara noastră, nici în creier. Roșul există numai atunci când noi, ca subiecți, interceptăm aceste mișcări. Este prin urmare imposibil să vorbim despre cum ajunge roșul să întâlnească ochiul sau sunetul do diez urechea?
Întrebarea este: Ce este o reprezentare de acest tip, unde se naște ea? Aceste întrebări abundă peste tot în filosofia secolului al XIX-lea. Schopenhauer a propus definiția „Lumea este reprezentarea noastră” [Nota 7]. Ce mai rămăne, în acest caz, pentru corpul exterior? Așa cum o reprezentare de culoare poate fi „creată” prin mișcare, la fel și percepția mișcării poate apărea în noi prin ceva care nu se mișcă. Să presupunem că lipim 12 instantanee ale unui cal în mișcare pe suprafața interioară a unui cilindru echipat cu 12 fante (crăpături) între aceste imagini. Dacă privim dintr-o parte la cilindrul rotitor, o să avem impresia că vedem mereu același cal și că picioarele sale se mișcă [Nota 8]. Organizarea noastră corporală poate induce impresia mișcării chiar atunci când, în realitate, obiectul respectiv nu se mișcă. În acest mod ceea ce noi numim mișcare se dizolvă în nimic.
Ce este deci materia? Dacă dezbrăcăm materia de culoare, mișcare, formă și de toate celelalte calități percepute senzorial, nu mai rămâne nimic. Dacă senzațiile „subiective” cum este culoarea, sunetul, căldura și mirosul care apar în conștiența individualităților ca un rezultat al stimulilor mediului trebuie căutate înăuntrul nostru, la fel trebuie căutate senzațiile „obiective”, primare, de formă și mișcare. Lumea exterioară dispare cornplet. Această stare de lucruri creează grave dificultăți pentru epistemologie [Nota 9].
Presupunând că toate calitățile obiectelor există în afara noastră, cum intră ele în noi? Unde este punctul în care exteriorul este transformat în interior? Dacă dezbrăcăm lumea exterioară de tot conținutul percepțiilor senzoriale, ea nu mai există. Epistemologia începe să semene cu baronul Münchhausen care încerca să se țină suspendat în aer ținându-se de propriul păr [Nota 10]. Pentru a explica senzațiile care apar în noi trebuie să presupunem că lumea exterioară există, dar trebuie să ne întrebăm cum anume ajung diferite aspecte ale acestei lumi înăuntrul nostru sub forma reprezentărilor?
Este necesar să formulăm această întrebare într-un mod diferit. Să considerăm câteva analogii care sunt necesare pentru descoperirea legăturii dintre lumea exterioară și senzațiile interioare. Să ne întoarcem la segmentul de dreaptă cu capetele sale A și B. Pentru a face aceste puncte să coincidă trebuie să ne mișcăm dincolo de prima dimensiune și să îndoim segmentul (figura 7).
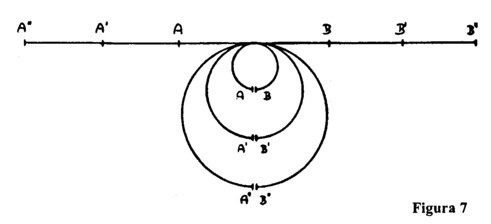
Să ne imaginăm acum că facem să coincidă aceste puncte în așa fel încât să se întâlnească sub linia originală. Putem trece apoi prin punctele suprapuse și să ne întoarcem la punctul de la care am plecat. Dacă segmentul original este scurt, cercul rezultat este mic, dar dacă curbăm segmente mai lungi în cercuri, punctul unde se întâlnesc capetele se mișcă tot mai departe de linia originală până când ajunge la distanța infinită. Curbura crește încet până când nu mai putem distinge cu ochiul liber circumferința cercului de o linie dreaptă (figura 8).
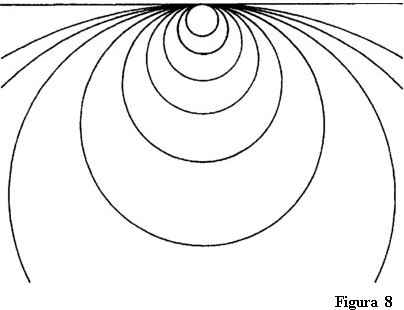
În mod asemănător, atunci când umblăm pe Pământ el apare ca fiind o suprafață plană, deși este rotund. Dacă ne imaginăm cele două jumătăți ale segmentului extinzându-se în infinit, cercul chiar coincide cu o linie dreaptă [Nota 11]. Astfel, o linie dreaptă poate fi interpretată ca un cerc al cărui diametru este infinit. Acum putem să ne imaginam că dacă ne mișcăm și mai departe de-a lungul liniei drepte în cele din urmă vom trece prin infinit și ne vom întoarce din cealaltă parte.
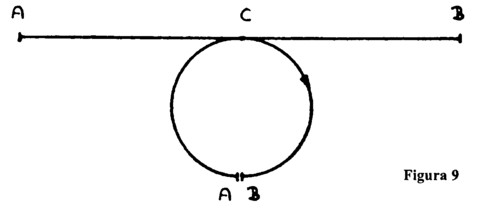
În locul unei linii să ne imaginăm o situație pe care o putem asocia cu realitatea. Să ne imaginăm că punctul C devine tot mai rece pe măsură ce se mișcă de-a lungul circumferinței cercului și se îndepărtează de punctul de plecare. Când trece prin limita inferioară A, B și începe călătoria de întoarcere pe cealaltă parte, temperatura începe să crească (figura 9).
Astfel, pe drumul de întoarcere punctul C întâlnește condiții care sunt opuse celor întâlnite în prima jumătate a călătoriei. Tendința de încălzire continuă până când este atinsă temperatura inițială. Procesul rămâne același indiferent cât de mare este cercul; căldura descrește inițial și apoi crește din nou. Și la linia care se extinde în infinit temperatura descrește într-o parte și crește în cealaltă. Acesta este un exemplu despre cum putem aduce viața și mișcarea în lume și începem să înțelegem lumea într-un sens mai înalt. Aici avem două activități mutual dependente. Atât cât privește observația senzorială, procesul care se mișcă spre dreapta nu are nimic de-a face cu procesul care se întoarce dinspre stânga, și totuși cele două sunt mutual dependente [Nota 12].
Și acum să punem în legătură obiectele lumii exterioare cu starea de răcire, iar senzațiile noastre interne cu starea de încălzire. Deși lumea exterioară și senzațiile noastre interne nu se află în legătură în mod direct prin nimic perceptibil cu simțurile, ele sunt legate și dependente una de alta în același fel ca și procesele pe care tocmai le-am descris. În sprijinul celor spuse despre relația lor putem folosi și metafora peceții și cerei. Pecetea lasă o impresie exactă, o copie a ei însăși în ceară chiar dacă nu rămâne în contact cu ceara și nu există transfer de substanță între ele. Ceara reține o impresie fidelă a peceții. Legătura dintre lumea exterioară și senzațiile noastre interioare este similară. Numai aspectul esențial este transmis. Un set de circumstanțe îl determină pe celălalt, dar nu are loc niciun transfer de substanță [Nota 13].
Văzând în acest fel legătura dintre lumea exterioară și impresiile noastre ne dăm seama că imaginile simetrice în oglindă sunt ca și mănușile dreapta și stânga. Pentru a le face să coincidă cu o mișcare continuă avem nevoie de o nouă dimensiune a spațiului. Dacă relația dintre lumea exterioară și impresiile interne este analogă cu relația dintre figurile care sunt imagini în oglindă, atunci și acestea pot fi făcute să coincidă numai cu ajutorul unei noi dimensiuni. Pentru a stabili o conexiune între lumea exterioară și impresiile interioare trebuie să trecem printr-o a patra dimensiune, fiind încă într-a treia. Numai acolo unde suntem uniți cu lumea exterioară și cu impresiile interioare putem descoperi ce au ele în comun. Ne putem închipui imagini-oglindă plutind într-o mare în care pot fi făcute să coincidă. Astfel ajungem, deși la început numai la nivelul gândirii, la ceva care este real dar transcende spațiul tridimensional. Pentru a face asta avem nevoie să dăm viață ideii noastre de spațiu.
Oskar Simony a încercat să folosească modele pentru a descrie formațiuni spațiale vitalizate [Nota 14]. Așa cum am văzut, putem să ne mișcăm pas cu pas de la spațiile cu nicio dimensiune până la imaginarea unui spațiu cvadridimensional. Spațiul cvadridimensional poate fi recunoscut cel mai ușor cu ajutorul imaginilor-oglindă sau a relațiilor de simetrie. Curbele cu noduri și panglicile bidimensionale oferă o altă metodă de a studia calitățile unice ale spațiului tridimensional empiric așa cum se raportează la spațiul cvadridimensional. Ce înțelegem prin relații de simetrie? Atunci când punem în legătură figuri spațiale apar anumite complicații: Aceste complicații aparțin numai spațiului tridimensional; ele nu apar în spațiul cvadridimensional [Nota 15].
Să încercăm câteva exerciții de gândire practică. Dacă tăiem un inel cilindric de-a lungul liniei mediane obținem două inele. Dacă răsucim o panglică cu 180° înainte de a-i lipi capetele, tăind-o apoi în lungul mijlocului panglicii, va rezulta un singur inel răsucit care nu se va separa. Dacă vom răsuci o panglică cu 360° înainte de a-i lipi capetele se vor separa două inele care trec unul prin interiorul celuilalt. Și, în sfârșit, dacă avem o panglică răsucită cu 720°, tăind-o, rezultă un nod [Nota 16]. Oricine care gândește la procese naturale știe că asemenea răsuciri au loc în natură. În realitate, toate formațiunile spațiale răsucite posedă asemenea forțe. Luați, spre exemplu, mișcarea Pământului în jurul Soarelui și mișcarea Lunii în jurul Pământului. Spunem că Luna descrie un cerc în jurul Pământului, dar dacă ne uităm mai atent ne dăm seama că de fapt descrie o linie care este răsucită în jurul orbitei Pământului, adică o spirală în jurul elipsei Pământului. Și apoi avem Soarele care se mișcă rapid prin spațiu, așa încât Luna mai face o mișcare spiralată în jurul Soarelui. Astfel, liniile de forță care se extind în spațiu sunt foarte complexe. Trebuie să realizăm că avem de-a face cu concepte spațiale complicate pe care le putem înțelege numai dacă nu încercăm să le fixăm, ci le permitem să rămână fluide.
Să recapitulăm ceea ce am discutat astăzi. Punctul nu are nicio dimensiune, dreapta are o singură dimensiune, suprafața două dimensiuni iar corpul solid are trei dimensiuni. Cum se raportează aceste concepte spațiale unul la celălalt? Imaginați-vă că sunteți o ființă care se poate mișca numai de-a lungul unei linii drepte. Ce fel de imagini spațiale pot avea asemenea ființe? Asemenea ființe ar fi capabile să perceapă numai puncte și nu propria lor dimensiune deoarece, dacă ar încerca să deseneze ceva în interiorul unei linii, punctele sunt singura opțiune. O ființă bidimensională ar fi capabilă să întâlnească numai linii, și astfel să distingă numai ființe unidimensionale. O ființă tridimensională, cum ar fi un cub, ar percepe numai ființe bidimensionale. Ființa umană poate percepe trei dimensiuni. Dacă tragem concluzia justă, trebuie să spunem că, așa cum o ființă unidimensională poate percepe numai puncte, o ființă bidimensională numai o dimensiune și o ființa tridimensională numai două dimensiuni, o ființă care poate percepe trei dimensiuni trebuie să fie cvadridimensională. Pentru că putem delimita ființele exterioare tridimensionale și putem manipula spații tridimensionale trebuie să fim ființe cvadridimensionale [Nota 17]. Așa cum un cub poate percepe numai două dimensiuni și nu propria tridimensionalitate, este, de asemenea, adevărat că ființele umane nu pot percepe a patra dimensiune în care trăim.