Ultima dată am încercat să obținem reprezentarea unei formațiuni spațiale cvadridimensionale reducând-o la trei dimensiuni. Mai întâi am convertit o figură tridimensională într-una bidimensională. Am substituit dimensiunile cu culori, construind imaginea noastră prin folosirea a trei culori pentru a reprezenta cele trei dimensiuni ale cubului. Apoi am desfașurat cubul în așa fel încât toate suprafețele s-au așezat în plan, rezultând șase pătrate ale căror laturi, diferit colorate, au reprezentat cele trei dimensiuni în spațiul bidimensional.
Apoi ne-am imaginat că transferăm fiecare pătrat în cea de a treia dimensiune, mișcându-l printr-o ceață colorată și permițându-i să reapară în cealaltă parte. Ne-am imaginat toate suprafețele pătrate mișcându-se prin și fiind colorate de pătratele de tranziție. Astfel am folosit culori pentru a încerca să înfățișăm cubul tridimensional în două dimensiuni. Pentru a reprezenta pătrate într-o singură dimensiune am folosit două culori diferite pentru laturile lor perechi; pentru a reprezenta un cub în două dimensiuni am folosit trei culori. Înfățișarea unei figuri cvadridimensionale în spațiul tridimensional cere o a patra culoare.
Apoi ne-am imaginat un cub cu trei culori de suprafață diferite în mod analog cu pătratul nostru cu două culori de muchie. Fiecare asemenea cub s-a mișcat printr-un cub de a patra culoare; adică a dispărut în a patra dimensiune sau culoare. În conformitate cu analogia lui Hinton, am făcut ca fiecare cub limită să se miște prin a patra culoare și să reapară în cealaltă parte în culoarea sa originală.
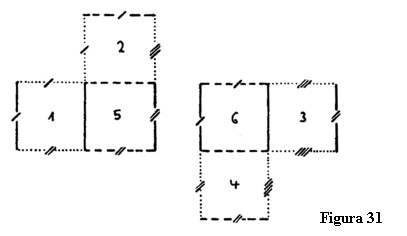
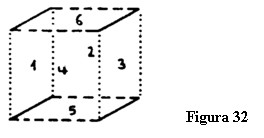
Acum aș vrea să vă dau o altă analogie. Vom începe din nou prin a reduce trei dimensiuni la două pentru a pregăti reducerea a patru dimensiuni la trei. Trebuie să ne imaginăm construind cubul din șase pătrate, dar în loc de a lăsa toate pătratele atașate atunci când le desfășurăm în plan le vom aranja diferit, așa cum este arătat în figura 31. Așa cum vedeți, am împărțit cubul în două sisteme a trei pătrate fiecare. Ambele grupuri sunt așezate în același plan. Trebuie să înțelegem unde este așezat fiecare grup când reasamblăm cubul. Pentru a reface cubul trebuie să plasez un grup deasupra celuilalt așa încât pătratul 6 să stea deasupra pătratului 5. Odată ce pătratul 5 este în poziție trebuie să ridic pătratele 1 și 2, în timp ce pătratele 3 și 4 trebuie să fie coborâte (figura 32). Atunci, perechile corespunzătoare segmentelor liniare ‒ adică cele de aceeași culoare (aici cu același număr și fel de liniuțe, așa cum se vede în figura 31) ‒ vor coincide. Aceste linii care sunt răspândite în spațiul bidimensional coincid atunci când facem tranziția spre spațiul tridimensional.
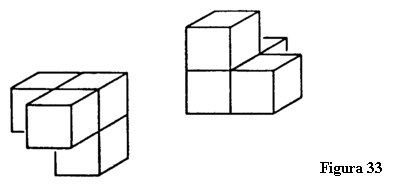
Pătratul constă din patru laturi, cubul din șase pătrate, iar domeniul cvadridimensional ar trebui să fie alcătuit atunci din opt cuburi [Nota 36]. Hinton numește această figură cvadridimensională tessarakt. Sarcina noastră de a pune aceste opt cuburi împreună într-un singur „cub” nu este simplă, dar pentru aceasta trebuie să-l facem pe fiecare să treacă prin a patra dimensiune. Când fac cu un tessarakt ceea ce am făcut cu un cub trebuie să respect aceeași lege. Trebuie să folosim analogia relației unei figuri tridimensionale cu contrapartea sa bidimensională pentru a descoperi relația unei figuri cvadridimensionale cu contrapartea sa tridimensională. În cazul unui cub desfășurat aveam două grupuri de trei pătrate. În mod similar, prin desfășurarea unui tessarakt în spațiul tridimensional rezultă două grupuri a câte patru cuburi care arată ca în figura 33. Metoda celor opt cuburi este foarte ingenioasă.
Trebuie să manevrăm cele patru cuburi în spațiul tridimensional la fel cum am manevrat pătratele în spațiul bidimensional. Priviți îndeaproape la ceea ce am făcut aici. Prin desfacerea unui cub în spațiul bidimensional a rezultat un grup de șase pătrate. Făcând operația corespunzătoare cu un tessarakt, rezultă un sistem de opt cuburi (figura 34). Am transferat reflecțiile noastre privitoare la spațiul tridimensional asupra celui cvadridimensional. Îmbinării pătratelor și suprapunerii muchiilor în spațiul tridimensional le corespund îmbinarea cuburilor și suprapunerea suprafețelor lor în spațiul cvadridimensional. Prin desfășurarea cubului în spațiul bidimensional au rezultat linii corespondente care s-au suprapus când am reconstruit cubul. Ceva similar se întâmplă cu suprafețele diferitelor cuburi ale tessarakt-ului. Prin desfășurarea unui tessarakt în spațiul tridimensional rezultă suprafețe corespunzătoare ale cuburilor respective care vor coincide mai târziu. Astfel, într-un tessarakt suprafața orizontală superioară a cubului 1 se află în același plan cu suprafața frontală a cubului 5 când ne mișcăm în cea de a patra dimensiune.
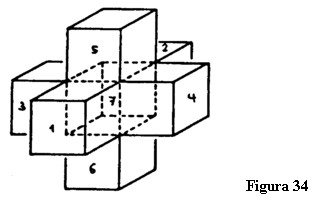
La fel, suprafața dreaptă a cubului 1 coincide cu suprafața frontală a cubului 4, suprafața stângă a cubului 1 coincide cu suprafața frontală a cubului 3 și suprafața inferioară a cubului 1 coincide cu suprafața frontală a cubului 6. Corespondențe similare există și în cazul celorlalte suprafețe. Când operația este completă cubul care rămâne este cubul 7, cubul interior care era înconjurat de celelalte șase cuburi [Nota 37].
Așa cum vedeți, este vorba încă o dată de găsirea analogiilor dintre a treia și a patra dimensiune. După cum am văzut într-una din figurile din conferința precedentă (figura 29), tot așa cum un al cincilea pătrat înconjurat de alte patru rămâne invizibil pentru cel care poate vedea numai în două dimensiuni, la fel se întâmplă, cu al șaptelea cub în acest caz. El rămâne ascuns vederii tridimensionale. Într-un tessarakt acest al șaptelea cub corespunde cu un al optulea cub, contrapartea sa în cea de a patra dimensiune.
Toate aceste analogii servesc pentru a ne pregăti pentru a patra dimensiune, întrucât nimic din concepția noastră obișnuită asupra spațiului nu ne forțează să adăugăm alte dimensiuni la cele familiare nouă. Urmând exemplul lui Hinton, am putea folosi culori și gândi cuburile puse laolaltă în așa fel încât să coincidă culorile corespunzătoare. Altfel decât prin asemenea analogii este aproape imposibil să dăm vreo sugestie despre felul în care trebuie să concepem o figură cvadridimensională.
Aș dori să vorbesc despre un alt fel de reprezentare a corpurilor cvadridimensionale în spațiul tridimensional care ar putea să vă facă să înțelegeți mai bine care este de fapt problema. Avem un octaedru care are opt fețe triunghiulare care formează între ele unghiuri obtuze (figura 35).
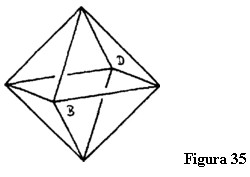
Vă rog să vă imaginați această figură și apoi să urmariți împreună cu mine următorul șir de gânduri. Vedeți, aceste muchii sunt intersecțiile dintre două suprafețe. De exemplu, două se intersectează de-a lungul lui AB și două de-a lungul lui EB. Singura diferență dintre un octaedru și un cub este unghiul format de două fețe alăturate. Când suprafețele se intersectează sub unghiuri drepte, așa cum se întâmplă în cub, figura care se formează trebuie să fie un cub. (Nota traducătorului: se referă probabil la fețe pătrate care se intersectează sub unghiuri drepte pentru că altminteri se poate obține în cel mai general caz un paralelipiped dreptunghic.) Când ele se intersectează sub unghiuri obtuze, așa cum se întâmplă aici se formează un octaedru. (Nota traducătorului: cred că este valabilă din nou aceeași observație, acum fiind vorba însă de suprafețe triunghiulare.) Făcând ca suprafețele să se intersecteze sub unghiuri diferite construim alte figuri geometrice [Nota 38].
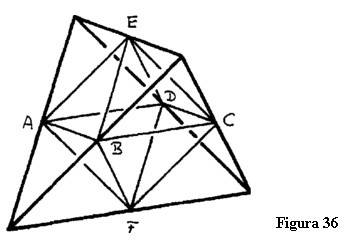
Să ne imaginăm mai departe un mod diferit de a face suprafețele unui octaedru să se intersecteze. Imaginați-vă că una din aceste suprafețe, cum este AEB, este extinsă în toate direcțiile și că suprafața inferioară, BCF, și suprafețele ADF și EDC, din spatele figurii, sunt extinse în mod similar. Aceste suprafețe extinse trebuie de asemenea să se intersecteze, și anume se intersectează potrivit unei duble simetrii. Când aceste suprafețe sunt extinse celelalte patru suprafețe originale ale octaedrului, ABF, EBC, EAD și DCF, sunt eliminate. Din cele opt suprafețe originale rămân doar patru și acestea patru formează un tetraedru care poate fi numit, de asemenea, jumătate de octaedru din cauză că jumătate din suprafețele octaedrului se intersectează. Nu este jumătate de octaedru în sensul că acesta se taie în două prin mijloc. Când sunt extinse celelalte suprafețe ale octaedrului până când se intersectează, ele formează, de asemenea, un tetraedru. Octaedrul original este intersecția acestor două tetraedre. În stereometrie sau în cristalografia geometrică, ceea ce este numit jumătate de figură este mai degrabă rezultatul înjumătățirii numărului de suprafețe decât al împărțirii figurii originale în două. Aceasta este foarte ușor de vizualizat în cazul unui octaedru [Nota 39]. Dacă vă imaginați un cub înjumătățit în același fel făcând ca una din suprafețe să se intersecteze cu o altă suprafață, veți obține întotdeauna un cub. Jumătate de cub este întotdeauna un alt cub. Din acest fenomen se poate trage o importantă concluzie, dar mai întâi aș dori să folosesc un alt exemplu [Nota 40].
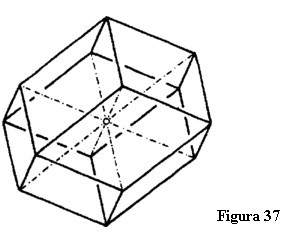
Avem un dodecaedru rombic (figura 37). Așa cum vedeți, suprafețele sale se intersectează sub anumite unghiuri. Avem, de asemenea, un sistem de patru fire ‒ le voi numi fire axiale ‒ care se îndreaptă în diferite direcții, adică sunt diagonale care unesc colțuri opuse ale dodecaedrului rombic. Aceste fire reprezintă sistemul de axe ale dodecaedrului rombic similar cu sistemul de axe pe care vi-l puteți imagina în cub [Nota 41].
Obtinem un cub atunci când într-un sistem de trei axe perpendiculare se pun în evidență suprafețe de intersectare prin aceea că în fiecare din aceste axe apar stagnări. Făcând ca axele să se intersecteze sub alte unghiuri se obține o altă formațiune geometrică. De exemplu, axele unui dodecaedru rombic se intersectează sub unghiuri care nu sunt drepte. Înjumătățind un cub obținem tot un cub [Nota 42]. Acest lucru este adevărat, însă numai pentru un cub. Atunci când se înjumătățește numărul suprafețelor unui dodecaedru rombic se obține, de asemenea, o formațiune spațială complet diferită [Nota 43].
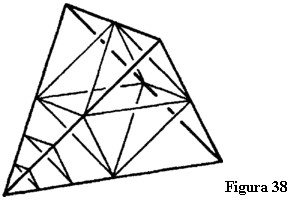
Și acum haideți să observăm cum se raportează un octaedru la un tetraedru. Lăsați-mă să vă arăt ce vreau să spun. Relația este clar aparentă dacă transformăm treptat un octaedru într-un tetraedru. Pentru acest scop să luăm un tetraedru și să-i tăiem unul dintre vârfuri, așa cum se arată în figura 38. Continuăm să tăiem porțiuni din ce în ce mai mari, până când secțiunile se intersectează pe muchiile tetraedrului. Forma care rămâne este un octaedru. Tăind vârfurile sub unghiuri corespunzătoare am transformat o figură spațială mărginită de patru plane într-o figură cu opt fețe.
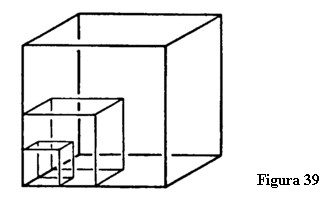
Ceea ce am făcut cu un tetraedru nu poate fi făcut cu un cub [Nota 44]. Un cub are proprietăți cu totul speciale prin aceea că este contrapartea spațiului tridimensional. Imaginați-vă întregul spațiu al Universului ca fiind structurat de trei axe perpendiculare una pe cealaltă. Inserarea de plane perpendiculare pe aceste axe produce întotdeauna un cub (figura 39). Din această cauză, ori de câte ori folosim termenul cub pentru a desemna cubul teoretic vorbim despre cub ca fiind contrapartea spațiului tridimensional. Așa cum tetraedrul este contrapartea unui octaedru prelungind jumătate din fețele octaedrului până când se intersectează, un cub individual este contrapartea întregului spațiu [Nota 45]. Dacă vă imaginați întregul spațiu ca fiind pozitiv, atunci cubul este negativ. Cubul este polar față de întregul spațiu. Cubul fizic este figura geometrică care corespunde efectiv întregului spațiu.
Să presupunem că în loc de un spațiu tridimensional mărginit de plane bidimensionale avem un spațiu mărginit de șase sfere care sunt figuri tridimensionale. Încep prin a defini un spațiu bidimensional cu ajutorul a patru cercuri secante, adică figuri bidimensionale. Acum imaginați-vă că aceste cercuri devin tot mai mari; adică razele lor cresc tot mereu și centrele devin tot mai depărtate. Cu timpul, cercurile se vor transforma în linii drepte (figura 40). Atunci în loc de patru cercuri avem patru linii drepte care se întretaie și un pătrat.
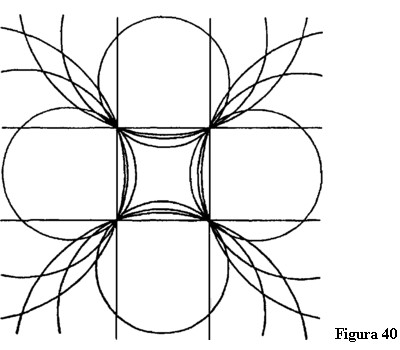
Acum, în loc de cercuri, imaginați-vă șase sfere formând ceva asemănător cu o mură (figura 41). Imaginați-vă că sferele devin tot mai mari, exact ca și cercurile. În cele din urmă, aceste sfere devin planele care definesc un cub, așa cum cercurile au devenit liniile care definesc un pătrat. Acest cub este rezultatul a șase sfere care au devenit plate. De aceea cubul este un caz particular al intersecției a șase sfere, așa cum pătratul este un caz special al intersectării a patru cercuri.
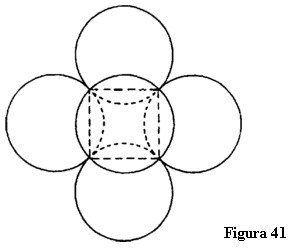
Atunci când vă dați seama clar că aceste șase sfere se aplatizează în plane corespunzând pătratelor pe care le-am folosit mai devreme pentru a defini cubul ‒ adică atunci când vizualizați o figură sferică fiind transformată într-una plată ‒ obțineți cea mai simplă figură spațială. Un cub poate fi imaginat ca rezultat al aplatizării a șase sfere secante.
Putem spune că un punct de pe un cerc trebuie să treacă prin a doua dimensiune pentru a ajunge la un alt punct de pe cerc. Dar dacă cercul a devenit atât de mare încât formează o linie dreaptă, orice punct de pe cerc poate ajunge la orice alt punct, mișcându-se numai prin prima dimensiune.
Să considerăm un pătrat care este marginit de figuri bidimensionale. Atât timp cât cele patru formațiuni care definesc pătratul sunt cercuri ele sunt bidimensionale. Odată ce devin linii drepte ele sunt unidimensionale.
Planele care definesc un cub se dezvoltă din figuri tridimensionale (sferele) prin aceea că o dimensiune este înlăturată din fiecare din cele șase sfere. Aceste suprafețe apar ca fiind dezdoite prin reducerea dimensiunilor lor de la trei la două. Și-au sacrificat astfel o dimensiune. Ele intră în a doua dimensiune sacrificând dimensiunea adâncimii. Astfel am putea spune că fiecare dimensiune a spațiului ia naștere prin sacrificarea dimensiunii imediat superioare.
Dacă avem o formă tridimensională cu limite bidimensionale și astfel reducem formele tridimensionale la două dimensiuni, trebuie să concluzionați din aceasta că dacă considerăm spațiul tridimensional trebuie să gândim la fiecare direcție ca fiind versiunea plată a unui cerc infinit. Apoi, dacă ne mișcăm într-o direcție, ne-am întoarce în cele din urmă la punctul inițial din direcția opusă. Astfel, fiecare dimensiune obișnuită a spațiului a apărut prin pierderea dimensiunii superioare următoare. Un sistem triaxial este inerent în spațiul nostru tridimensional. Fiecare din cele trei axe perpendiculare a sacrificat dimensiunea următoare pentru a deveni dreaptă.
În acest fel obținem, așadar, spațiul tridimensional prin îndreptarea fiecăreia din cele trei direcții axiale. Inversând procesul, fiecare element al spațiului poate fi de asemenea curbat din nou. Atunci ar rezulta următorul șir de gânduri: când curbați o formațiune unidimensională figura care rezultă este bidimensională; o formațiune bidimensională devine tridimensională. Și, în final, curbând o figură tridimensională se obține o figură cvadridimensională. Astfel spațiul cvadridimensonal poate fi imaginat ca spațiu tridimensional curbat [Nota 46].
În acest punct putem face tranziția de la neviu la viu. În această curbare puteți găsi forme spațiale care revelează această tranziție de la neviu la viu. La trecerea spre tridimensional, găsim un exemplu special de spațiu cvadridimensional; el a devenit plat. Pentru conștiența umană moartea nu este nimic mai mult decât curbarea tridimensionalului în cvadrimensional. În privința corpului fizic luat în sine, lucrurile stau invers: moartea este aplatizarea a patru dimensiuni în trei.